Stabilitatea navei

Stabilitatea navei

Stabilitatea este proprietatea navei de a reveni la pozitia initiala de echilibru, dupa disparitia cauzei care a determinat scoaterea ei din aceasta pozitie.

In studiul teoretic al stabilitatii se utilizeaza sistemul de axe de coordonate Oxyz.

Nava, considerata ca un solid rigid raportat la sistemul de axe de coordonate Oxyz, poate sa efectueze 6 miscari, deci are 6 grade de libertate, adica:

miscarea dupa axa longitudinala;

miscarea dupa axa transversala;

miscarea dupa axa verticala;

miscarea de rotatie in jurul unei axe verticale;

miscarea de rotatie in jurul unei axe longitudinale;

miscarea de rotatie in jurul unei axe transversale.

Miscarea navei dupa directia axei longitudinale sau transversale si miscarea de rotatie a navei in jurul unei axe verticale nu determina modificarea conditiilor initiale de echilibru.

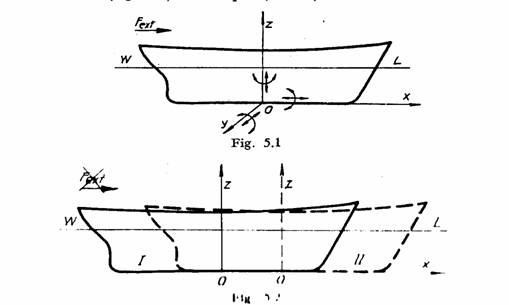
Miscarea navei dupa directia axei verticale, sub actiunea unei forte exterioare, determina o noua pozitie de echilibru definita de asemenea de o plutire dreapta. Daca este asigurata etansarea corpului, la disparitia actiunii fortei exterioare, nava revine intotdeauna la pozitia initiala de echilibru definita de plutirea dreapta WL.

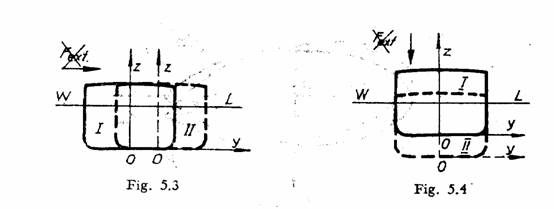
Miscarile de rotatie in jurul unor axe longitudinale si transversale duc la modificarea celei de-a doua conditii de echilibru si la aparitia momentelor stabilitatii.

La incetarea actiunii momentelor exterioare, nava poate sa revina la pozitia initiala de echilibru, sa ramana in pozitia de echilibru inclinat sau sa se incline in sensul imprimat initial.

Stabilitatea studiaza fenomenele ce insotesc inclinarile navei in plan transversal si longitudinal.

1.1.  Stabilitatea navei la unghiuri mici de inclinare (<15s)

In studiul stabilitatii initiale sinusul si tangenta unghiului de inclinare se aproximeaza cu valoarea unghiului exprimata in radiani, iar cosinusul cu 1.

Inclinari si plutiri izocarene. Teorema lui Euler. Teorema deplasarii centrului de carena.

Pe timpul inclinarilor deplasamentul ramane constant si corespunde situatiei de incarcare a navei. De asemenea, volumul carenei ramane constant.

Inclinarile navei, carora le corespunde acelasi volum de carena, se numesc inclinari izocarene.

Plutirile corespunzatoare inclinarilor izocarene se numesc plutiri izocarene.

Teorema lui Euler: Doua plutiri izocarene succesive, pentru un unghi infinit de mic de inclinare, se intersecteaza dupa o dreapta ce trece prin centrele lor geometrice.

Pentru demonstratie se considera nava reprezentata prin sectiunea transversala ce include centrul F al plutirii initiale drepte WL, precum si o portiune din suprafata acestei plutiri. De mentionat ca . Fie , marimea momentului exterior, care produce inclinarea definita de unghiul infinit mic . Acestei inclinari ii corespunde plutirea .

Se presupune, prin reducere la absurd, ca plutirile nu se intersecteaza dupa dreapta ce trece prin F, ci dupa o axa ce trece prin punctul . Volumul , care intra in apa in urma inclinarii, se numeste volumul ongletului imers. Volumul , care iese din apa in urma inclinarii navei, se numeste volumul ongletului emers.

Avem:

.

Se noteaza cu ariile partii suprafetei plutirii din dreapta, respectiv din stanga axei . Pentru calculele volumelor se considera cilindrii elementari situati la distantele fata de , la aceeasi distanta a fata de Ox si avand bazele de arie .

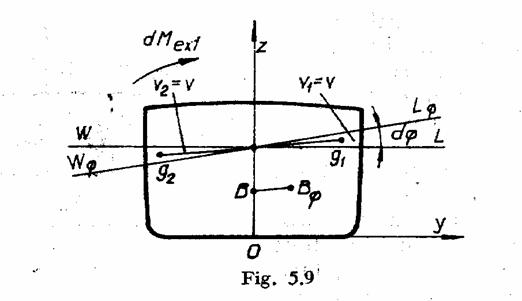
Egalitatea este adevarata daca: .

Deci, dreapta de intersectie trece prin punctul F, care in cazul inclinarii infinit mici este centrul geometric al ambelor plutiri.

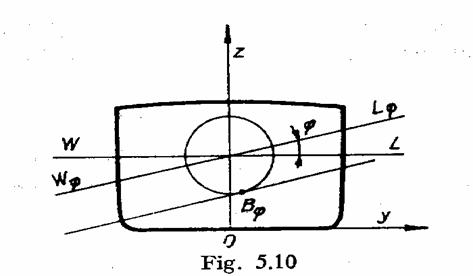
Fie acum nava reprezentata in ¤, avand pozitia initiala dreapta WL si centrul de carena B. Sub actiunea momentului exterior, de marime , ea se inclina in plan transversal cu unghiul . In urma inclinarii plutirea navei devine , iar centrul de carena se deplaseaza in . Volumele celor doua onglete sunt egale, deci . Deplasarea centrului de carena este cauzata de deplasarea volumului v din centrul geometric al ongletului emers in centrul geometric al ongletului imers.

Teorema: La inclinarile infinit mici ale navei, centrul de carena se deplaseaza dupa o directie paralela cu dreapta ce trece prin centrele geometrice ale celor doua onglete si are marimea proportionala cu , respectiv cu volumul v ce se deplaseaza din ongletul emers in ongletul imers si invers proportionala cu volumul carenei V.

Linia descrisa de centrul de carena la inclinarea navei intr-un plan oarecare se numeste linia centrelor de carena.

Proiectia pe planul de inclinare a liniilor centrelor de carena se numeste curba centrelor de carena.

Proprietate: Tangenta dusa intr-un punct la curba centrelor de carena este paralela cu plutirea care admite pe drept centru de carena.

Teoremele si aceasta ultima proprietate enuntate pentru inclinarile in plan transversal, sunt valabile si in cazul inclinarilor in plan longitudinal.

Metacentre. Raze metacentrice. Momente ale stabilitatii sau de redresare. Inaltimi metacentrice.

Cazul inclinarilor transversale

Se considera nava reprezentata prin sectiunea sa in ¤, avand pozitia initiala dreapta WL, careia ii corespunde centrul de carena B. Fie , marimea momentului exterior care

produce inclinarea definita de unghiul infinit mic . Acestei inclinari ii corespunde plutirea . Centrul de carena se deplaseaza din B in descriind curba centrelor de carena. Se duc tangentele la curba centrelor de carena in B si . Normalele la aceste tangente in B si se intersecteaza in punctul denumit metacentru transversal.

Metacentrul transversal este centrul de curbura al curbei centrelor de carena pentru inclinarile transversale.

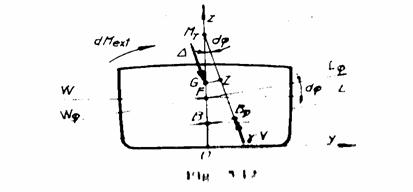
Pozitia metacentrului transversal este definita de cota .

Cota a metacentrului transversal este distanta de la la PB.

Inclinarea navei fiind mica, arcul se aproximeaza cu coarda, care se considera confundata cu tangenta la curba centrelor de carena in .

Raza metacentrica transversala este distanta de la centrul de carena la metacentrul transversal sau altfel spus este raza de curbura a curbei centrelor de carena corespunzatoare unei inclinari transversale infinit mici.

se calculeaza din triunghiul , care este dreptunghic:

.

Prin deplasarea centrului de carena din B in , se modifica directiile de actiune ale fortei de impingere Arhimede si de deplasament, luand nastere cuplul care defineste momentul stabilitatii transversale. Pentru inclinarea infinit mica:

,

unde este bratul cuplului si se calculeaza din triunghiul dreptunghic :

.

Inaltimea metacentrica transversala este distanta de la metacentrul transversal, corespunzator inclinarilor nule, la centrul de greutate.

,

in care: este distanta de la centrul de carena la centrul de greutate pentru inclinarea nula.

.

Cazul inclinarilor longitudinale

Se considera nava reprezentata prin sectiunea sa in PD, avand pozitia initiala dreapta WL, careia ii corespunde centrul de carena B. Fie , marimea momentului exterior care produce inclinarea definita de unghiul . Acestei inclinari in corespunde plutirea . Centrul de carena se deplaseaza din B in , descriind curba centrelor de carena in plan longitudinal.

Metacentrul longitudinal este centrul de curbura al curbei centrelor de carena pentru inclinarile longitudinale si are pozitia definita prin cota .

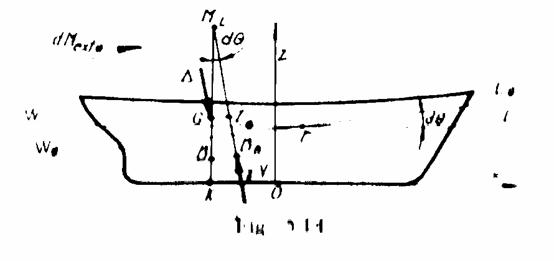
Raza metacentrica longitudinala este distanta de la centrul de carena la metacentrul longitudinal sau, altfel spus, este raza de curbura a curbei centrelor de carena, corespunzatoare unei inclinari longitudinale infinit mici.

,

unde este inaltimea metacentrica longitudinala.

Inaltimea metacentrica longitudinala este distanta de la metacentrul longitudinal, corespunzator inclinarii nule, la centrul de greutate.

.

Momentul stabilitatii de forma si de greutate. Formulele metacentrice ale stabilitatii initiale. Momentul unitar de banda si de asieta. Scara de incarcare

Momentul stabilitatii de forma si de greutate. Cazul inclinarilor transversale.

Se considera nava reprezentata prin sectiunea sa in ¤, avand plutirea initiala dreapta WL si centrul de carena B. Fie , marimea momentului exterior care inclina nava in plan transversal cu unghiul infinit mic . Plutirea definita de acest unghi este . Fenomenul aparitiei momentului stabilitatii transversale se descompune ipotetic in doua etape.

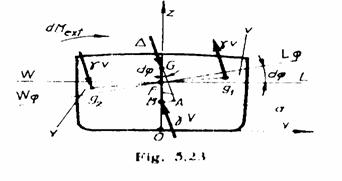
In prima etapa se presupune ca, in urma inclinarii navei, volumul carenei nu-si modifica forma, deci centrul de carena ramane in B. Cele doua forte, una de deplasament, aplicata in G si cealalta de impingere Arhimede, aplicata in B, actioneaza perpendicular pe dand nastere cuplului care defineste momentul stabilitatii de greutate:

.

In a doua etapa se considera ca pe nava deja inclinata se produce deplasarea volumului de apa v, din centrul al ongletului emers in centrul al ongletului imers. Aceasta deplasare determina aparitia a doua forte de marime , aplicate in , perpendiculare pe si de semne contrare. Cuplul celor doua forte defineste momentul stabilitatii de forma:

.

Momentul stabilitatii de forma si de greutate. Cazul inclinarilor longitudinale.

Se procedeaza similar si se obtine:

.

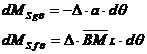
Momentul stabilitatii de forma este parte componenta a momentului stabilitatii si este definit de cuplul de forte ce apare ca urmare a deplasarii volumului de apa v, din ongletul emers in ongletul imers.

Momentul stabilitatii de greutate este parte componenta a momentului stabilitatii si este definit de cuplul fortelor de deplasament si impingere Arhimede, care actioneaza perpendicular pe plutirea inclinata, pastrandu-si punctele de aplicatie corespunzatoare plutirii initiale.

Formulele metacentrice ale stabilitatii

Pentru unghiuri mici finite , avem:

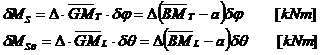
In unele situatii, cand , momentele stabilitatii se pot calcula cu urmatoarele formule fara a se aproxima sinusul cu valoarea unghiului exprimata in radiani si astfel avem:

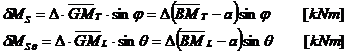
Moment unitar de banda si de asieta. Scara de incarcare.

Momentul unitar de banda este momentul exterior care inclina nava in plan transversal cu un unghi .

Pentru stabilirea formulei de calcul a momentului unitar de banda se pune conditia de echilibru, corespunzatoare pozitiei inclinate definite de unghiul :

.

Daca in aceasta formula se face se obtine:

.

Momentul unitar de asieta este momentul exterior, care inclina nava in plan longitudinal producandu-i o asieta .

Asieta navei este diferenta dintre pescajele prova si pupa.

Pentru stabilirea formulei de calcul a momentului unitar de asieta se pune conditia de echilibru, corespunzatoare pozitiei inclinate definite de unghiul :

.

Se observa ca:

.

Avem:

Scara de incarcare este un tabel in care sunt trecute valorile deplasamentului Δ, deplasamentului , deplasamentului unitar , momentului unitar de banda si momentului unitar de asieta pentru diferite pescaje cuprinse intre LB si CWL.

Influenta greutatii specifice a apei asupra stabilitatii initiale si asietei navei

Daca si diferenta dintre cele doua greutati specifice este infinit mica, adica , atunci avem:

.

Variatia a volumului carenei corespunzatoare lui este:

.

Influenta greutatii specifice a apei asupra stabilitatii initiale. Cazul inclinarilor transversale

Marimea asupra careia se manifesta influenta greutatii specifice a apei este inaltimea metacentrica transversala.

Prin diferentiere avem:

.

Deoarece si relatia de mai sus devine:

.

Discutie:

Daca , deci nava trece intr-o apa cu greutate specifica mai mare, atunci:

pentru si stabilitatea initiala transversala scade;

pentru si stabilitatea initiala transversala creste;

pentru si stabilitatea initiala transversala ramane neschimbata.

Daca , deci nava trece intr-o apa cu greutatea specifica mai mica, atunci:

pentru si stabilitatea initiala transversala creste;

pentru si stabilitatea initiala transversala scade;

pentru si stabilitatea initiala transversala ramane neschimbata.

La variatii mici ale pescajului bordurile se considera verticale si si avem:

.

Noua inaltime metacentrica transversala este:

Influenta greutatii specifice a apei asupra stabilitatii initiale. Cazul inclinarilor longitudinale

In ipoteza bordurilor verticale si daca se tine cont de faptul ca , avem:

.

Noua inaltime metacentrica transversala este:

Influenta greutatii specifice a apei asupra asietei navei

Variatia infinit mica a volumului carenei determina deplasarea a centrului de carena dupa directia axei Ox. Ca urmare a acestei deplasari apare un moment exterior, de marime , care produce inclinarea navei in plan longitudinal cu unghiul . Inclinarea determina aparitia momentului stabilitatii .

La echilibru: 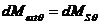, adica: .

Daca

In cazul inclinarilor mici finite avem:

Influenta greutatii specifice a apei asupra asietei a navei este:

Deplasarea de greutati la bordul navei

Pe timpul deplasarilor de greutati, deplasamentul navei nu se modifica si in consecinta nici pescajul mediu.

Deplasarea dupa directia axei longitudinale

Se considera nava reprezentata prin sectiunea sa in PD, avand plutirea initiala dreapta WL si centrul de greutate situat in punctul G. Fie q, marimea greutatii care se deplaseaza dupa Ox din punctul in punctul . Conform teoremei deplasarii centrul de greutate al navei se deplaseaza din G in G' pe distanta definita de:

.

Deplasarea centrului de greutate este insotita de modificarea pozitiei punctului de aplicatie al fortei de deplasament. Acest fenomen se poate echivala prin reprezentarea a doua forte de marime Δ: una aplicata in G avand directia si sensul axei Oz, iar alta aplicata in G' avand directia si sensul contrar axei Oz.

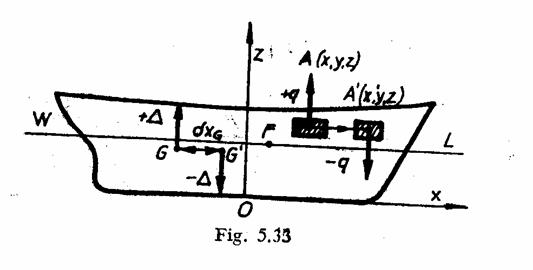
Cele doua forte paralele, cu marimile egale si de semne contrare, dau nastere cuplului ce defineste momentul exterior, care inclina nava in plan longitudinal cu unghiul .

Marimea momentului exterior este: .

Prin inclinarea navei se deplaseaza centrul de carena inspre partea inclinarii, ceea ce duce la aparitia momentului stabilitatii longitudinale: .

Se pune conditia de echilibru:

.

Cu valoarea unghiului se poate trasa noua plutire a navei.

Intrucat este mic si apar dificultati la masurarea lui, mai usor se poate trasa plutirea daca se cunosc pescajele la cele doua extremitati ale navei.

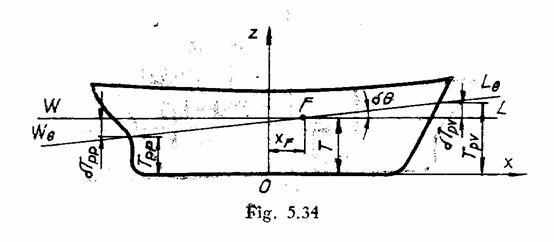
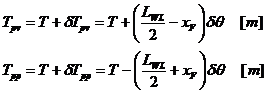
sau:

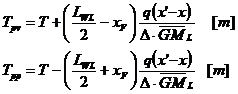
Deplasarea greutatilor la bord dupa directia axei longitudinale determina modificarea asietei navei.

Deplasarea dupa directia axei transversale

Se considera nava reprezentata prin sectiunea sa in ¤. Greutatea de marime q se deplaseaza dupa Oy din in punctul .

Se determina deplasarea centrului de greutate:

si unghiul de inclinare transversala:

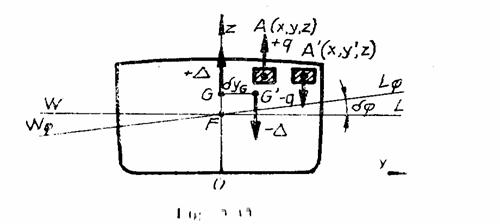
Intrucat , valoarea unghiului este mare comparativ cu si permite trasarea plutirii finale cu destula exactitate fara a mai fi nevoie sa se calculeze pescajele in borduri.

Deplasarea greutatilor la bord dupa directia axei transversale determina inclinarea navei in plan transversal.

Deplasarea dupa directia axei verticale

Se considera nava reprezentata prin sectiunile sale in PD si ¤. Greutatea de marime q se deplaseaza dupa Oz din in punctul .

Se obtine deplasarea centrului de greutate: .

Intrucat modificarea pozitie punctului de aplicatie al fortei de deplasament nu determina aparitia vreunui cuplu, in urma deplasarii greutatii dupa directia axei Oz nu se produce nici un fel de inclinare a navei. In schimb se modifica stabilitatea initiala transversala si longitudinala.

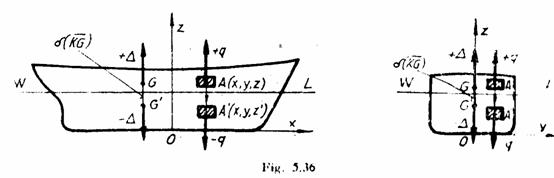
Deoarece pe timpul deplasarii greutatii volumul carenei nu variaza, metacentrul ramane in pozitie initiala, deci , . Se diferentiaza si se obtine:

. Aceasta relatie este valabila pentru deplasarea unei greutati infinit mici.

Pentru o greutate mica finita avem:

.

Astfel ca avem noile inaltimi metacentrice:

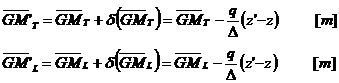
La deplasarea unei greutati pe verticala in jos stabilitatea initiala a navei creste, iar la deplasarea unei greutati pe verticala in sus stabilitatea initiala a navei scade.

Influenta greutatilor suspendate, rostogolitoare si incarcaturilor lichide cu suprafete libere asupra stabilitatii initiale a navei.

Influenta greutatilor suspendate

In practica exploatarii navei pot aparea situatii care impun transportul unor greutati suspendate. Prezenta acestora la bord influenteaza negativ stabilitatea initiala a navei. Astfel se considera nava reprezentata prin sectiunea sa in ¤, raportata la sistemul de axe yOz si avand plutirea initiala dreapta. Fie q marimea unei greutati suspendate in punctul A prin intermediul firului de lungime . Daca greutatea nu ar fi suspendata, sub actiunea momentului exterior de marime , nava se inclina cu unghiul care rezulta din conditia de echilibru: .

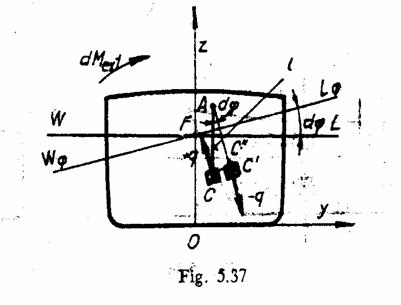
Cum greutatea este suspendata, pe timpul inclinarii, ea se deplaseaza pe distanta astfel incat . Deplasarea greutatii pe timpul inclinarii este deci insotita de modificarea punctului de aplicatie si directiei de actiune a fortei . Acest fenomen poate fi echivalat prin reprezentarea a doua forte, de marime q, perpendiculare pe , de semne contrare si avand punctele de aplicatie in C respectiv C'. Cuplul celor doua forte defineste un moment de inclinare a carui marime este:

.

Inclinarea navei cu unghiul , in prezenta greutatii suspendate, se obtine prin actiunea unui moment exterior a carui marime , adica: .

Momentului exterior ii corespunde momentul stabilitatii . Intrucat , avem: .

Se pune conditia de echilibru: .

In cazul inclinarilor longitudinale se procedeaza la fel si se obtine:

Prezenta la bord a unei greutati suspendate determina o variatie negativa a inaltimilor metacentrice, proportionala cu marimea greutatii si lungimea firului de suspensie.

Reducerea influentei negative asupra stabilitatii initiale, pe timpul transportului unor greutati suspendate, se realizeaza prin folosirea elementelor de suspensie de lungime cat mai mica.

Influenta greutatilor rostogolitoare

Greutatile rostogolitoare sunt greutatile neamarate de la bordul navei.

Prezenta greutatilor rostogolitoare influenteaza negativ stabilitatea initiala. Aceasta influenta se evidentiaza considerand sectiunea transversala a unei nave cu bordurile duble si dublul fund curbat. Fie greutatea de marime q aflata initial in punctul C. In urma inclinarii navei cu unghiul greutatea se rostogoleste ajungand in punctul C'. Directiile de actiune ale fortei corespunzatoare pozitiei drepte si inclinate a navei se intersecteaza in punctul A. Se noteaza cu raza de curbura a curbei descrise de centrul greutatii rostogolitoare pe timpul inclinarii infinit mici.

pentru inclinarile transversale:

.

pentru inclinarile longitudinale:

.

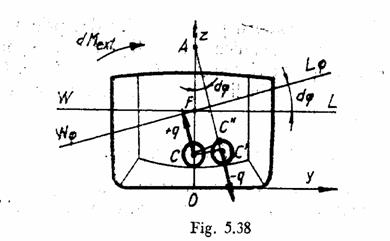
Prezenta la bord a unei greutati rostogolitoare determina o variatie negativa a inaltimilor metacentrice, proportionala cu marimea greutatii si cu raza de curbura a portiunii din suprafata pe care se rostogoleste.

Pentru determinarea punctului A necesar definirii lui , in cazul rostogolirii unei greutati pe o suprafata plana, din centrul greutatii aflate in contact cu bordul, se duce o normala la plutirea . Punctul A rezulta din intersectia acestei normale cu normala dusa din C la WL.

Anularea influentei negative a greutatilor rostogolitoare asupra stabilitatii initiale se realizeaza prin amararea acestora.

Influenta incarcaturilor lichide cu suprafete libere

Incarcaturile lichide se intalnesc la bordul tuturor categoriilor de nave.

Influenta incarcaturilor lichide asupra stabilitatii navei se manifesta numai cand compartimentele nu sunt complet pline, deci prezinta suprafete libere.

Se considera o nava reprezentata prin sectiunea sa in ¤, avand plutirea initiala dreapta WL. Fie v, volumul lichidului de greutate specifica dintr-un tanc neumplut complet. Corespunzator plutirii initiale a navei, suprafata libera este paralela cu WL, iar forta de greutate a lichidului are marimea , punctul de aplicatie in centrul geometric c al volumului v, directia si sensul contrar axei Oz.

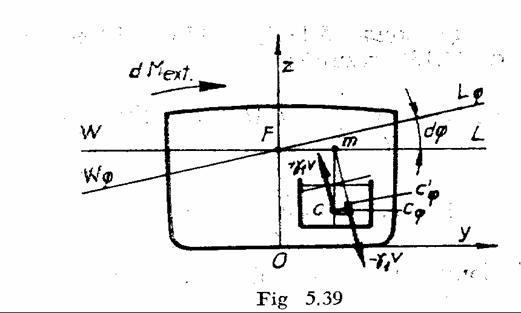
In lipsa suprafetei libere, sub actiunea momentului exterior, de marime , nava se inclina cu unghiul care rezulta din conditia de echilibru.

In urma inclinarii, daca lichidul are suprafata libera, aceasta isi modifica pozitia devenind paralela cu . Punctul de aplicatie al fortei de greutate se deplaseaza din c in .

Se obtine momentul de inclinare:

,

unde are semnificatia de raza metacentrica transversala pentru volumul lichidului din tanc si este: , in care este momentul de inertie al suprafetei libere a lichidului din tanc fata de axa centrala longitudinala de inertie proprie.

Astfel ca: .

Inclinarea navei cu unghiul , in prezenta suprafetei libere, se obtine prin actiunea unui moment exterior a carui marime , adica:

.

Momentului exterior definit mai sus ii corespunde momentul stabilitatii . Se pune conditia de echilibru:

.

Se ajunge la relatia:

.

Pentru inclinarile longitudinale se obtine:

,

unde este momentul de inertie al suprafetei libere fata de axa centrala transversala de inertie proprie, iar este greutatea specifica a apei in care se afla nava.

Prezenta la bord a unei incarcaturi lichide cu suprafata libera determina o variatie negativa a inaltimilor metacentrice, proportionala cu greutatea specifica a lichidului si cu momentele de inertie ale suprafetei libere fata de axele centrale de inertie proprii.

Influenta ambarcarii (debarcarii) de greutati asupra stabilitatii initiale

Ambarcarea (debarcarea) de greutati mici

Se considera nava reprezentata prin sectiunile sale in PD si ¤, avand plutirea initiala dreapta WL, definita de pescajul T. Fie q, marimea greutatii si , punctul de pe nava in care aceasta urmeaza sa fie ambarcata.

Ambarcarea greutatii la bord evitand inclinarile navei.

In aceasta prima etapa se ambarca greutatea in punctul . Dupa ambarcare se produce o variatie a pescajului mediu, iar plutirea navei devine W'L'.

Intrucat greutatea introdusa la bord, inainte de a ajunge in A se deplaseaza dupa directia axei verticale, se modifica inaltimile metacentrice.

Pentru determinarea variatiei inaltimii metacentrice transversale se poate scrie:

,

in care: sunt variatiile razei metacentrice transversale, cotei centrului de carena si cotei centrului de greutate.

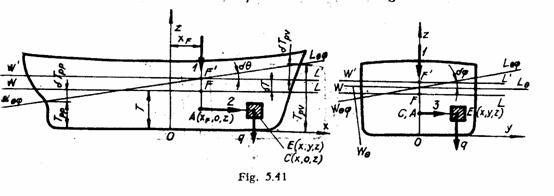
Variatia razei metacentrice transversale este data de:

,

unde: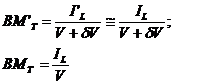

Se obtine: .

Variatia inaltimii metacentrice este:

,

formula fiind valabila pentru ambarcare cat si pentru debarcare.

La sfarsitul primei etape, inaltimea metacentrica transversala devine:

.

Planul orizontal, a carui pozitie este definita de cot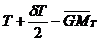a , se numeste plan neutru sau plan limita pentru stabilitatea transversala.

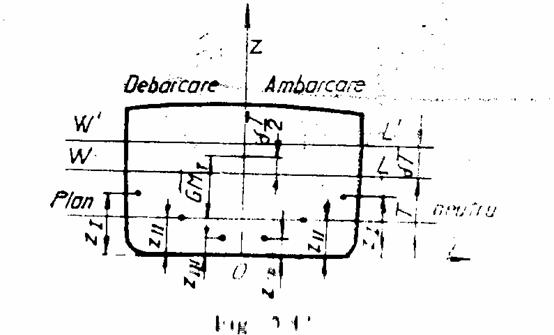
La ambarcare, lui q i se asociaza semnul +, deci termenul din fata parantezei este pozitiv si se disting urmatoarele trei situatii:

daca punctul de ambarcare are cota ; , deci stabilitatea scade;

daca punctul de ambarcare are cota ; , deci stabilitatea ramane neschimbata;

daca punctul de ambarcare are cota ; , deci stabilitatea creste.

La ambarcarea unei greutati deasupra planului neutru, stabilitatea initiala transversala scade; in planul neutru ramane neschimbata, iar sub planul neutru creste.

La debarcarea lui q i se asociaza semnul -, deci termenul din fata parantezei este negativ si se disting urmatoarele trei situatii:

daca punctul de debarcare are cota ; , deci stabilitatea creste;

daca punctul de debarcare are cota ; , deci stabilitatea ramane neschimbata;

daca punctul de debarcare are cota ; , deci stabilitatea scade.

La debarcarea unei greutati de deasupra planului neutru, stabilitatea initiala transversala creste, din planul neutru ramane neschimbata si de sub planul neutru, scade.

Pentru a se evita scaderea stabilitatii initiale transversale se impune ca ambarcarea marfurilor la bord sa se faca de jos in sus, iar debarcarea de sus in jos.

Pentru determinarea influentei ambarcarii (debarcarii) asupra stabilitatii initiale longitudinale procedand analog se obtin:

;

.

Planul orizontal, a carui pozitie este definita de cota , se numeste plan neutru sau plan limita pentru stabilitatea longitudinala.

Deoarece , planul neutru pentru stabilitatea longitudinala este situat mult sub nava.

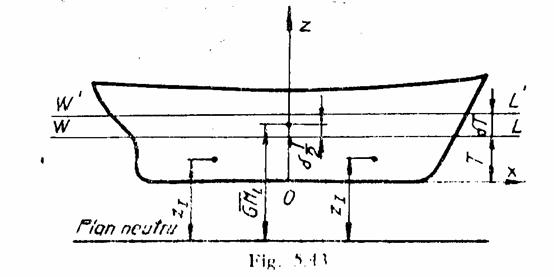
La ambarcare, lui q i se asociaza semnul +, deci termenul din fata parantezei este pozitiv si cand punctul de ambarcare are cota si , deci stabilitatea scade.

La debarcare, lui q i se asociaza semnul -, deci termenul din fata parantezei este negativ si cand punctul de debarcare are cota si , deci stabilitatea creste.

La ambarcarea unei greutati la bord, stabilitatea longitudinala scade si la debarcare, creste.

Deplasarea greutatii dupa directia axei longitudinale.

In aceasta etapa greutatea se deplaseaza dupa axa Ox din in . Nava se inclina in plan longitudinal cu unghiul .

Cunoscand acest unghi se traseaza plutirea care se intersecteaza cu W'L' in F'.

Deplasarea greutatii dupa directia axei transversale.

In aceasta etapa greutatea se deplaseaza dupa Oy din in . Nava se inclina in plan transversal cu unghiul .

Acum se poate trasa plutirea inclinata in plan transversal, care se raporteaza la .

Ambarcarea (debarcarea) de greutati mari

Calculul ambarcarii (debarcarii) unei greutati mari cuprinde doua etape:

determinarea modificarii pescajului mediu si inaltimilor metacentrice, pentru care se utilizeaza diagrama de carene drepte, astfel:

[m]

  [m]

[m]

unde primul semn corespunde ambarcarii de greutati la bord, iar al doilea semn corespunde cazului debarcarii.

determinarea unghiurilor de inclinare longitudinala si transversala.

1.2.  Stabilitatea navei la unghiuri mari de inclinare

Stabilitatea la unghiuri mari studiaza inclinarile transversale statice si dinamice care depasesc 15s.

Intrucat in mod practic inclinarile longitudinale nu depasesc 15s, ele nu sunt incluse in studiul stabilitatii la unghiuri mari.

Inclinarea statica apare la actiunea lenta a momentului exterior si este caracterizata printr-o viteza unghiulara constanta.

Inclinarea dinamica apare la actiunea brusca a momentului exterior si este caracterizata printr-o viteza unghiulara variabila in timp; prin urmare aceasta inclinare este insotita de aparitia acceleratiei.

3.2.1. Stabilitatea statica la unghiuri mari de inclinare

Stabilitatea statica la unghiuri mari studiaza marimea si semnul momentului stabilitatii transversale si relatia dintre acesta si momentul exterior in cazul inclinarilor care depasesc 15s.

Expresiile analitice ale coordonatelor centrului de carena si metacentrului. Curba centrelor de carena si metacentrelor

Fie yOz, sistemul de axe de coordonate corespunzator sectiunii transversale care include centrul de carena. Pentru plutirea initiala dreapta sunt calculate: centrul de carena si metacentrul transversal . Sub actiunea momentului exterior de marime , centrul de carena se deplaseaza in punctul , iar metacentrul transversal in .

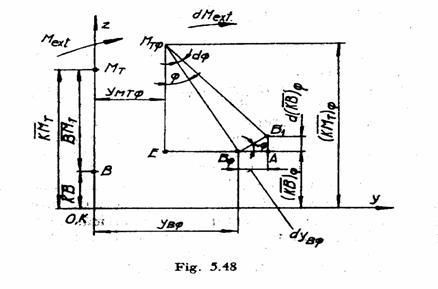
In continuare se vor determina coordonatele acestor doua puncte. Pentru aceasta, se presupune ca sub actiunea unui moment exterior de marime , nava se inclina suplimentar cu unghiul infinit mic . In urma inclinarii suplimentare centrul de carena se deplaseaza din in , iar metacentrul ramane in . Deplasarea a centrului de carena rezulta din deplasarile elementare: . Din triunghiul dreptunghic se scrie:

.

Din triunghiul dreptunghic avem:

;

.

Integrand pe intervalul se obtine: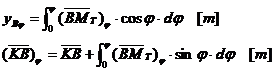

Coordonatele metacentrului transversal sunt:

;

.

Bratul stabilitatii statice. Momentul stabilitatii corespunzator unghiurilor mari de inclinare

Bratul stabilitatii statice pentru unghiul de inclinare se noteaza cu si este distanta dintre suportul fortei de deplasament si suportul fortei de impingere Arhimede.

Exista patru modalitati de deducere a formulei de calcul a bratului stabilitatii statice.

Se vor prezenta doar doua din cele patru modalitati.

Se considera sistemul de axe de coordonate yOz, corespunzator sectiunii transversale care include centrul de carena. Pentru plutirea initiala dreapta se scrie: ; si . In urma inclinarii navei cu unghiul , centrul de carena si metacentrul transversal se deplaseaza in si respectiv . Daca din G se duce , atunci bratul stabilitatii statice pentru unghiul este . In scopul stabilirii formulei de calcul, se face urmatoarea constructie grafica:

din B se duce si ;

din se duce , deci ;

din I se duce ;

din se duce ;

din G se duce .

Astfel avem: .

Din triunghiurile dreptunghice BPI, , GBL, avem:

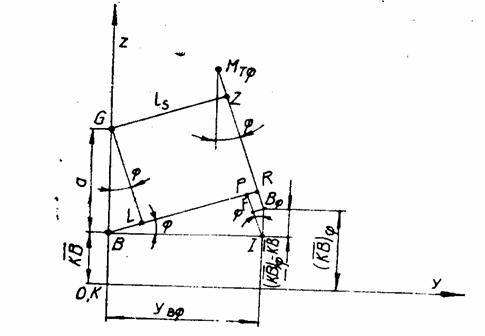
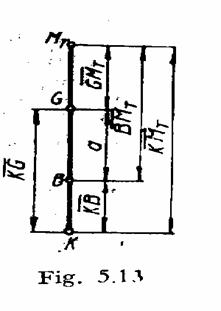
Bratul stabilitatii statice este:

.

Se considera nava reprezentata prin sectiunea sa in planul transversal care include

centrul de carena, avand plutirea initiala dreapta WL. Sub actiunea momentului de marime nava se inclina cu unghiul iar plutirea ei devine .

Momentul stabilitatii se poate scrie: .

este momentul stabilitatii de greutate si este:

este momentul stabilitatii de forma si este: .

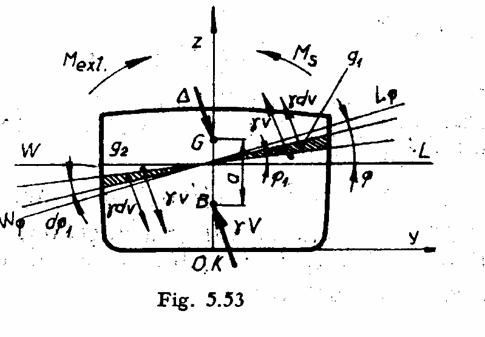
Astfel, bratul stabilitatii statice este: si este totdeauna pozitiv.

Diagrama stabilitatii statice. Proprietati

Reprezentarea grafica a functiei sau pentru se numeste diagrama stabilitatii statice.

Diagrama stabilitatii statice corespunzatoare inclinarilor navei intr-un bord are urmatoarele puncte caracteristice:

originea ;

maximul sau ;

punctul de apus (declin) ;

un punct oarecare de pe diagrama sau .

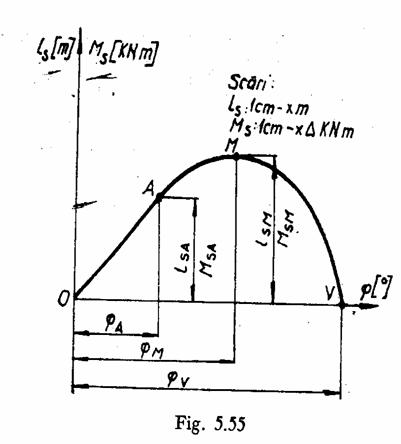
Diagrama stabilitatii statice se imparte in doua portiuni:

portiunea crescatoare de la O la M;

portiunea descrescatoare de la M la V.

este unghiul maxim de inclinare la care nava, lasata libera, revine in pozitia initiala de echilibru.

este unghiul de inclinare care, de regula, corespunde intrarii puntii in apa.

Functia sau este impara, adica:

P1: Daca prin punctul se duce tangenta la diagrama stabilitatii statice si dreapta orizontala, atunci segmentul definit de punctele de intersectie ale verticalei situate la fata de A cu cele doua, determina inaltimea metacentrica la scara lui .

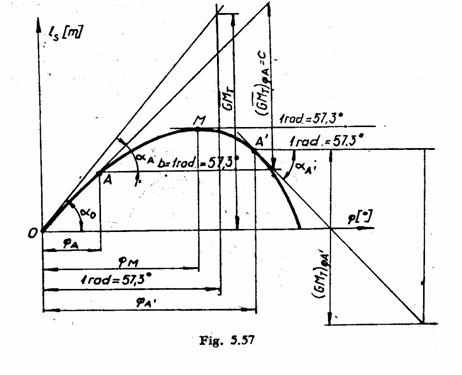
P2: Pe portiunea initiala tangenta in origine la diagrama se suprapune cu diagrama.

P3: Aria suprafetei definite de graficul functiei , axa si verticala corespunzatoare unghiului reprezinta lucrul mecanic al stabilitatii pentru aceasta inclinare a navei.

Aria suprafetei definite de graficul functiei si axa reprezinta lucrul mecanic total al stabilitatii corespunzator inclinarii navei intr-un bord si se numeste rezerva de stabilitate dinamica.

3.2.2. Stabilitatea dinamica la unghiuri mari de inclinare

Stabilitatea dinamica la unghiuri mari studiaza marimea si semnul lucrului mecanic al stabilitatii si relatia dintre acesta si lucrul mecanic exterior in cazul inclinarilor care depasesc 15s.

Lucrul mecanic exterior. Lucrul mecanic al stabilitatii sau de redresare. Bratul stabilitatii dinamice

Bratul stabilitatii dinamice corespunzator unghiului de inclinare reprezinta variatia distantei dintre centrul de greutate si centrul de carena masurat dupa directiile fortelor aplicate in aceste puncte.

Lucrul mecanic exterior consumat pentru inclinarea navei cu unghiul se noteaza cu .

Conditia de echilibru dinamic este: , unde:

este lucrul mecanic al stabilitatii.

Bratul stabilitatii dinamice este: .

Calculul bratului stabilitatii dinamice

M1:

M2: Se face constructia grafica, dupa care se masoara pe , din punctul Z spre , segmentul si avem:

.

Din triunghiurile dreptunghice BGL, BPI, avem:

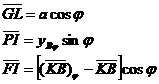
Bratul stabilitatii dinamice este: .

Diagrama stabilitatii dinamice. Proprietati

Reprezentarea grafica a functiei sau pentru se numeste diagrama stabilitatii dinamice.

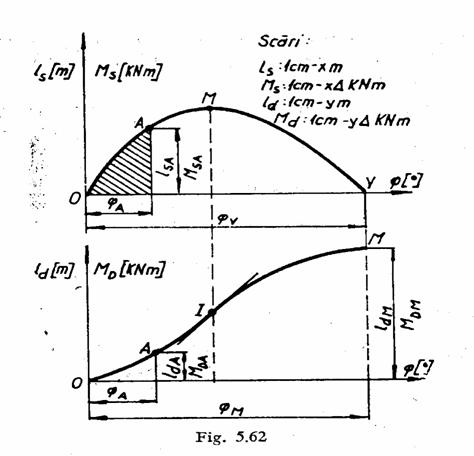
Punctele caracteristice ale diagramei stabilitatii dinamice sunt:

originea ;

punctul de inflexiune sau ;

punctul de maxim sau ;

un punct oarecare de pe diagrama sau .

P1: Graficul functiei admite axa ca tangenta in origine.

P2: Functia sau este para, adica: sau .

P3: La unghiul corespunzator punctului M de maxim al diagramei stabilitatii statice, diagrama stabilitatii dinamice are un punct I de inflexiune.

P4: Bratul stabilitatii dinamice corespunzator punctului A, de abscisa , reprezinta aria suprafetei de sub diagrama stabilitatii statice pana la .

P5: La unghiul corespunzator punctului V de apus al diagramei stabilitatii statice, diagrama stabilitatii dinamice are un punct M de maxim.

P6: Daca prin punctul se duce tangenta la diagrama stabilitatii dinamice si dreapta orizontala, atunci segmentul definit de punctele de intersectie ale verticalei situate la fata de A cu cele doua drepte determina la scara lui .

3.2.3. Probleme practice ce pot fi rezolvate cu ajutorul diagramei stabilitatii statice si dinamice

De regula, la rezolvarea problemelor cu ajutorul diagramelor stabilitatii, se folosesc graficele functiilor: .

Studiul echilibrului navei supuse actiunii unui moment exterior constant

Inclinarea navei pana la unghiul se produce intr-un anumit interval de timp, deci . Din studiul echilibrului static si dinamic al navei supuse actiunii unui moment exterior, a carui marime este constanta in timp, rezulta ca marimea momentului exterior ramane aceeasi la orice unghi de inclinare: .

Studiul echilibrului static

Conditia de echilibru static este: .

Graficul functiei este reprezentat pe diagrama stabilitatii statice. Graficul functiei este o dreapta paralela cu axa .

In punctul de intersectie a graficului functiei pentru cu diagrama stabilitatii statice se duce tangenta la diagrama si orizontala. Daca unghiul format de tangenta cu orizontala este pozitiv, atunci punctul este de echilibru stabil; daca unghiul este negativ sau nul, atunci punctul este de echilibru instabil.

Studiul echilibrului dinamic

Echilibrul dinamic al navei presupune respectarea conditiei: .

Graficul functiei este reprezentat pe diagrama stabilitatii dinamice. Daca , atunci lucrul mecanic exterior este: , unde este unghiul de inclinare in radiani.

Din aceasta ultima formula se observa ca graficul functiei este o dreapta ce trece prin originea sistemului de axe.

In punctul de intersectie a graficului functiei pentru cu diagrama stabilitatii dinamice se duce tangenta la diagrama si orizontala. Se noteaza cu unghiul format de tangenta cu orizontala si cu unghiul format de graficul functiei cu orizontala. Daca echilibrul dinamic este stabil; daca echilibrul dinamic este instabil.

Studiul echilibrului navei supuse actiunii unui moment exterior variabil

Studiul echilibrului static

Conditia de echilibru static: .

Graficul functiei este reprezentat pe diagrama stabilitatii statice. Peste el se suprapune graficul functiei , care de data aceasta este o curba oarecare. In punctele 1, 2, 3, 4 de intersectie ale celor doua grafice este indeplinita conditia de echilibru static.

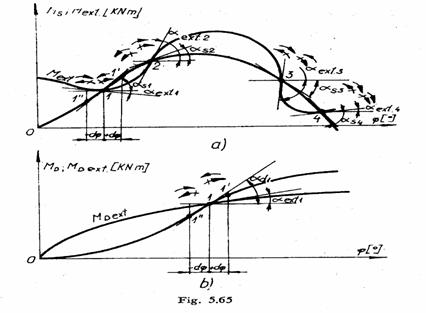
In punctul de intersectie a graficelor functiilor , , pentru , se duc tangentele la ele, care formeaza cu orizontala unghiurile: . Daca , punctul este de echilibru static stabil; daca , punctul este de echilibru static instabil.

Punctele 1 si 3 sunt de echilibru static stabil, iar 2 si 4 sunt puncte de echilibru static instabil.

Studiul echilibrului dinamic

Conditia de echilibru dinamic: .

Graficul functiei este reprezentat pe diagrama stabilitatii dinamice. Peste el se suprapune graficul functiei , avand forma unei curbe oarecare. Cele doua grafice se intersecteaza in punctul 1, unde este indeplinita conditia de echilibru dinamic.

In punctul de intersectie a graficelor functiilor , pentru se duc tangentele la ele, care formeaza cu orizontala unghiurile: . Daca , punctul este de echilibru dinamic stabil; daca , punctul este de echilibru dinamic instabil.

Punctul 1 este punct de echilibru dinamic stabil.

Determinarea unghiului de inclinare statica si dinamica a navei supuse actiunii unui moment exterior constant

Metoda cu diagrama stabilitatii statice

Peste graficul functiei se traseaza la aceeasi scara graficul functiei care, pentru este o dreapta paralela cu axa .

La inclinarea statica a navei, punctului de intersectie a celor doua grafice ii corespunde unghiul .

La inclinarea dinamica, la aplicarea brusca a momentului exterior nava se inclina pana in punctul , unde este indeplinita conditia de echilibru dinamic care se mai poate scrie sub forma: .

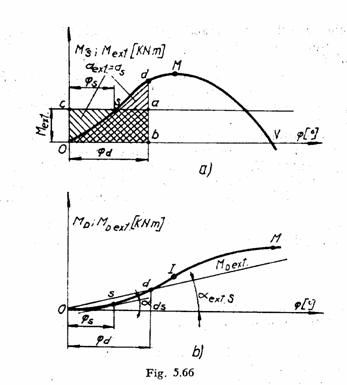
Punctului ii corespunde unghiul de inclinare dinamica a navei.

Inclinarea navei pana in si revenirea spre , unde , se face cu viteza unghiulara variabila in timp si este insotita de aparitia momentelor fortelor de inertie. Aceste momente determina cateva miscari oscilatorii ale navei in jurul lui , cu amplitudini din ce in ce mai mici inainte de stabilizarea sa in acest punct.

La inclinarea dinamica initiala definita de unghiul , nava poate sa-si piarda stabilitatea; in acest caz ea nu mai revine in .

Metoda cu diagrama stabilitatii dinamice

Momentul exterior constant, reprezentat pe diagrama stabilitatii statice, determina lucrul mecanic .

Peste graficul functiei se traseaza la aceeasi scara graficul functiei care este o dreapta ce trece prin originea sistemului de axe de coordonate. Punctului , de intersectie a reprezentarii grafice a celor doua functii, ii corespunde unghiul de inclinare dinamica a navei.

Avem: .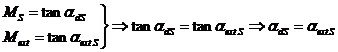

In cazul de fata este unghiul pe care il face graficul functiei cu axa .

Pentru a se respecta relatia este necesar sa se gaseasca punctul , in care tangenta la este paralela cu .

Punctul astfel gasit determina unghiul de inclinare statica a navei.

Determinarea unghiului de inclinare statica si dinamica a navei supuse actiunii unui moment exterior variabil

Metoda cu diagrama stabilitatii statice

Peste graficul functiei se traseaza la aceeasi scara graficul functiei , care pentru , este o curba.

Punctului , de intersectie a celor doua reprezentari grafice ale functiilor, ii corespunde unghiul de inclinare statica a navei.

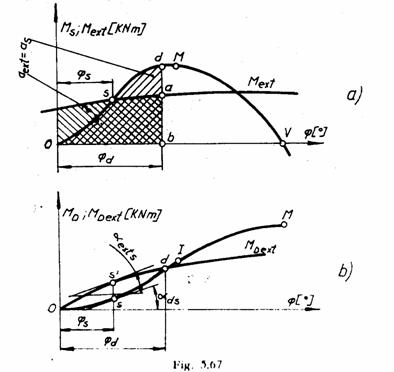
Punctul , caruia ii corespunde unghiul de inclinare dinamica, este stabilit astfel incat sa fie indeplinita conditia .

Metoda cu diagrama stabilitatii dinamice

Peste graficul functiei se traseaza la aceeasi scara graficul functiei care, pentru este o curba.

Punctului , de intersectie a celor doua grafice, ii corespunde unghiul de inclinare dinamica a navei.

Unghiul de inclinare statica trebuie sa asigure respectarea conditiei .

Pentru determinarea unghiului de inclinare statica se cauta punctele si astfel incat:

segmentul ;

tangenta la in sa fie paralela cu tangenta la in .

Segmentului ii corespunde unghiul de inclinare statica a navei.

Cu diagrama stabilitatii statice se poate determina valoarea exacta a unghiului de inclinare statica si valoarea aproximativa a unghiului de inclinare dinamica pentru nava supusa actiunii unui moment exterior constant sau variabil.

Cu diagrama stabilitatii dinamice se poate determina valoarea aproximativa a unghiului de inclinare statica si valoarea exacta a unghiului de inclinare dinamica pentru nava supusa actiunii unui moment exterior constant sau variabil.

Determinarea momentului dinamic maxim pe care il suporta nava

Metoda cu diagrama stabilitatii statice

Se considera diagrama stabilitatii statice. Se traseaza pe aceasta diagrama o dreapta orizontala astfel incat sa existe relatia . Distanta de la axa pana la aceasta orizontala reprezinta momentul dinamic maxim pe care il suporta nava. Sub actiunea acestuia nava se inclina pana in punctul caruia ii corespunde unghiul . Punctul este si de echilibru static, deci nava ramane in acest punct.

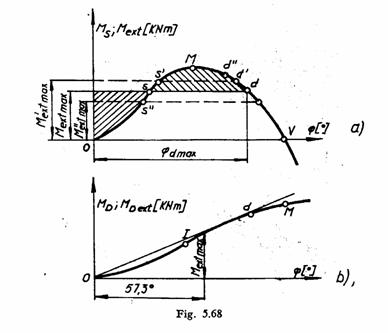
Metoda cu diagrama stabilitatii dinamice

Se duce din originea sistemului de axe de coordonate tangenta la diagrama stabilitatii dinamice si se obtine punctul . Aceasta dreapta reprezinta graficul functiei data de un moment exterior constant, iar este ultimul punct in care se mai asigura conditia de echilibru dinamic.

Determinarea momentului dinamic admisibil

Se face cu diagrama stabilitatii statice.

Punctul in care se stabileste nava, dupa inclinarea dinamica produsa de , se afla pe ramura descrescatoare a diagramei stabilitatii statice si este de echilibru instabil. Momentul dinamic admisibil este momentul exterior care aplicat brusc inclina nava pana intr-un punct situat pe ramura crescatoare a diagramei stabilitatii statice.

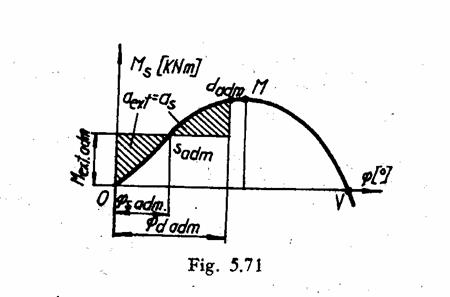
Determinarea se face astfel:

prin punctul , situat pe diagrama stabilitatii statice in stanga maximului M al acesteia, se duce o verticala;

se traseaza apoi peste diagrama o dreapta orizontala astfel incat ; distanta de la axa la aceasta orizontala reprezinta la scara diagramei.

Momentului dinamic admisibil ii corespund punctele , respectiv unghiurile de inclinare statica si dinamica.

se utilizeaza la verificarea stabilitatii navei sub actiunea dinamica a momentelor exterioare.