|
|
|
BIOSTATISTICA
CUPRINS:
1. Tema
2. Tabelul datelor initiale
3. Formarea distributiei empirice unidimensionala a diametrului de baza si prelucrari primare
3.1. Stabilirea numarului de clase
3.2. Determinarea amplitudinii clasei
3.3. Gruparea observatiilor in clase si formarea distributiei empirice
3.4. Reprezentari grafice
Histograma frecventelor absolute
Poligonul frecventelor absolute
Ogiva frecventelor absolute cumulate
3.5. Interpretari
4. Determinarea indicilor de pozitie ai distributiei empirice a diametrului de baza
4.1. Calcului mediei aritmetice
4.2. Determinarea mediilor de ordin superior
4.3. Determinarea medianei (analitic si grafic)
4.4. Determinarea modului (analitic si grafic)
4.5. Interpretari
5. Determinarea momentelor centrate de ordin 1-4 prin intermediul momentelor simple
5.1. Calculul momentelor simple
5.2. Determinarea momentelor centrate si aplicarea corectiilor lui Sheppard
6. Calculul indicelor de variatie ai distributiei empirice a diametrului de baza
6.1. Determinarea amplitudinii de variatie
6.2. Calculul variantei
6.3. Calculul abaterii standard si al abaterii standard al mediei aritmetice
6.4. Calculul coeficientului de variatie
6.5. Interpretari
7. Determinarea valorilor indicilor de forma ai distributiei empirice a diametrului de baza
7.1. Indicele asimetriei si eroarea acestuia
7.2. Indicele excesului si eroarea acestuia
7.3. Interpretari
8. Comparatie intre distributia experimentala si unele distributii teoretice
8.1. Ajustarea distributiei experimentale a diametrului de baza dupa legea distributiei teoretice normale
8.2. Controlul normalitatii prin testul de ajustare
8.3. Folosirea distributiei teoretice Charlier tip A pentru ajustarea distributiei experimentale a diametrului de baza
8.4. Test de ajustare pentru distributia Charlier tip A
8.5. Reprezentari grafice si interpretari
9. Determinarea intervalelor de incredere a mediilor aritmetice pentru trei probe referitoare la caracteristica diametru de baza
9.1. Constituirea celor trei probe si determinarea principalilor indicatori statistici
9.2. Analiza oportunitatii eliminarii din sirul statistic a observatiilor extreme
9.3. Determinarea efectiva a intervalelor de incredere ale mediilor aritmetice
9.4. Interpretari
10. Compararea mediilor aritmetice a celor trei probe
10.1. Examinarea semnificatiei diferentei dintre variantele probelor folosind testul Ficher
10.2. Examinarea semnificatiei diferentei dintre mediile aritmetice prin testul Student
11. Analiza simpla a variantei
11.1. Pregatirea datelor pentru analiza simpla a variantei
11.2. Analiza simpla a variantei
11.3. Testarea semnificatiei diferentelor dintre mediile aritmetice ale celor trei probe
12. Analiza corelatiei
12.1. Formarea distributiei empirice bidimensionale a caracteristicilor diametru de baza si grosimea dubla a cojii
12.2. Calculul coeficientului de corelatie pentru legatura corelativa anterioara si stabilirea semnificatiei acestuia
12.3. Determinarea intensitatii legaturii corelative intre cresterea pe radiala pe 10 ani si diametrului de baza pentru o proba cu N=20 arbori
12.3.1. Calculul coeficientului de corelatie r si determinarea semnificatiei
acestuia
12.3.2. Calculul coeficientului de corelatie a rangurilor si determinarea semnificatiei acestuia
13. Analiza regresiei
13.1. Determinarea ecuatiei de regresie liniare simple pentru legatura corelativa dintre grosimea dubla a cojii si diametrul de baza
13.2. Determinarea ecuatiei de regresie pentru legatura corelativa dintre cresterea radiala pe 10 ani si diametrul de baza
13.2.1. Determinarea parametrilor prin ecuatia de regresie lineare prin metoda celor mai mici patrate
13.2.2. Determinarea parametrilor ecuatiei de regresie neliniare de gradul II
13.2.3. Comparatii intre cele doua ecuatii de regresie
13.3.
Determinare ecuatiei de regresie multiple liniare de
forma
14. Interpretari de ansamblu si concluzii finale
1. TEMA
A. Sa se analizeze structura unui arboret de Moid in varsta de 70 de ani, folosind metode de statisticii matematice potrivit observatiilor inregistrate in tabelul datelor initiale si urmarind cuprinsul prezentat anterior.
B. Sa se stabileasca prin metode ale statisticii matematice, semnificatia diferentelor dintre trei esantioane de volume egale.
2. Date initiale
d(cm)
h(m)
d(cm)
h(m)
d(cm)
h(m)
d(cm)
h(m)
d(cm)
h(m)
57.1
40.5
42
31.7
48
34.5
48
37.2
54
44.6
58.0
40.7
30
27.2
55
38.5
36
33.5
40
35.5
42.0
37.1
55
39.2
52
36.4
37
36.
54
43
42.8
37.5
49
37.5
44
32.6
30
31
43
42
42.0
36.6
48
36
38
40
48
38.5
35
28
40.8
38.6
46
34.4
44
34
54
43
35
32
39.4
38.
35
30
36
28.2
44
34
34
32
52.0
41
41
33.8
47
41
56
38
38
31
36.0
32
39
35.4
44
35
40
36.5
46
42
44.0
37
42
33.2
67
43
49
36
46
36.6
48
34.5
52.5
38.9
42
27.8
60
44
43
32
28
28.5
55
39.2
68
43
36
30
34
30
53
39.5
37
30.3
42
34
40
33
42
36.5
65
41.7
38
35.6
44
35
49
40
58
40.5
50
40
51
44
52
39
40
32
62
44
51
38.2
28.5
25
42
36.5
54
44
39
33
57
39.7
59
39
32
32
32
28.4
46
36.6
41
33.3
35
31.5
56
41
40
37.2
42
35
62
41.5
43
35
47
38.5
32
25.9
42
36.2
35
28.5
50
38
47
37.5
54
44.6
45
37
50
39.2
55
40
47
37
40
30
47
37
62
44
53
39.8
47
34.8
40
32.8
39
36
47
35
52
38
49
38
32
31
43
33.6
33
31.2
45
35.4
49
36
54
45
51
38.8
43
34.2
63
40.4
44
34.5
44
35.5
64
43.
37
36.5
49
40.5
40
36
42
35
57
39.2
40
29
36
30
41
33.4
66
43.
39
38
52
38
35.5
31.4
36
27
40
34.2
3. Formarea distributiei empirice a diametrelor de baza ale arborilor si prelucrarii primare
3.1 Estimarea numarului de clase (k)
Pentru estimarea numarului de clase este nevoie ca datele ce urmeaza a fi prelucrate sa fie grupate in clase. Gruparea in clase se face in functie de diametrul de baza . Initial se stabileste un numar provizoriu de clase, conform tabelului de echivalenta dintre numarul de unitati N si numarul de clase k.
k
= 8.14
N
50 100 500
k
8 10 13
3.2 Determinarea amplitudinii clasei (a)
Marimea clasei se determina in functie de amplitudinea de variatie W si numarul provizoriu de clase formate k.
W = Xmax. -Xmin. W -
amplitudinea de variatie
W=68,0-28,0=40,0 a=40/8=5 a=4.0
3.3 Gruparea observatiilor in clase si formarea distributiei empirice unidimensionale
Pentru o cat mai usoara prelucrare a datelor, valorile experimentale se dispun in serii de distributii. O serie de distributie este formata din doua siruri de valori: un sir al valorilor experimentale si un sir ce poarta denumirea de frecvente. Acestea pot fi absolute si relative. Astfel:
Frecventa absoluta: - simpla reprezinta numarul de unitati statistice incluse in acea
clasa
- cumulata reprezinta un sir de valori ce se obtine prin cumularea
frecventelor absolute corespunzatoare claselor
Frecventa relativa: - simpla se determina efectuand raportul intre frecventa absoluta
simpla si volumul populatiei respective
- cumulata reprezinta un sir de valori ce se obtine prin cumularea
frecventelor relative corespunzatoare claselor
Tabel nr. 2
Nr.
crt.
Val. experimentale
Punctaj
Frecvente
limite
( cm )
centre
( cm )
absolute
relative
simple
cumulat
simple
cumulat
1
26.1-30.0
28
4
4
0.028777
0.028777
2
30.1-34.0
32
...
7
11
0.05036
0.079137
3
34.1-38.0
36
16
27
0.129496
0.208633
4
38.1-42.0
40
27
54
0.208633
0.417266
5
42.1-46.0
44
20
74
0.143885
0.561151
6
46.1-50.0
48
21
95
0.151079
0.71223
7
50.1-54.0
52
16
111
0.122302
0.834532
8
54.1-58.0
56
12
123
0.086331
0.920863
9
58.1-62.0
60
5
128
0.035971
0.956835
10
62.1-66.0
64
4
132
0.028777
0.985612
11
66.1-68.0
68
2
134
0.014388
1
Total
134
1
Suma frecventelor relative trebuie sa fie egala cu 1.
3.4. Reprezentari grafice
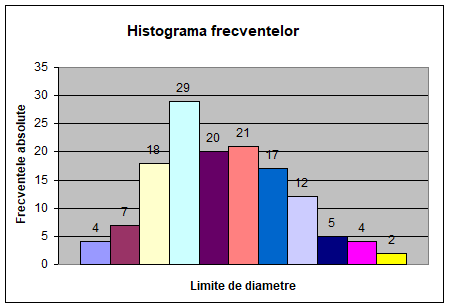
3.4.1 Histograma frecventelor absolute
3.4.2 Poligonul frecventelor absolute
3.4.3 Ogiva frecventelor absolute cumulate
3.4.1 Histograma frecventelor absolute
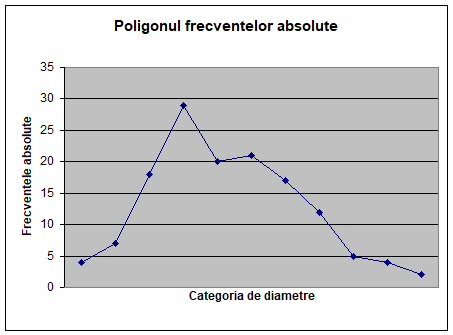
3.4.1 Poligonul frecventelor absolute
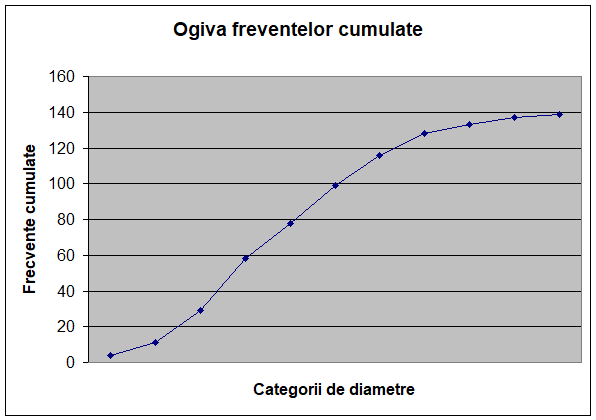
3.4.3 Ogiva frecventelor absolute cumulate
3.5 Interpretari
Pentru estimarea numarului de clase (k) ne-am folosit de metoda polaritatii,obtinand un numar de 12 clase ceea ce este permis in lucrarile din silvicultura,intrucat un nu ar mai mic de 10 clase ar duce la o precizie mai mica in analiza ezperimentala. Amplitudinea clasei s-a dovedit a fi egala cu 5, insa s-a rotunjit cu 4 deoarece calculele ar fi realizate mai usor.
In baza calculelor efectuate,putem spune ca majoritatea valorilor experimentale sunt grupate in jurul clasei de diametre 40,in numar de 29 de valori. Cele mai mici valori sunt situate in cadrul clasei de diametre 64 cu numai 2 valori.
4. Determinarea indicilor de pozitie ai distributiei empirice a diametrului de baza
4.1. Calculul mediei aritmetice.
Media aritmetica se calculeaza cu ajutorul formulei pentru valori grupate in clase:
=45.34
unde : - media
aritmetica
ni - frecventa absoluta simpla
xi - centrul clasei de diametre
__
4.2. Determinarea mediilor de ordin superior ( Xp, Xc )
Determinarea se face cu formula:
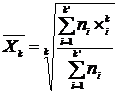
p=4623 c=4736
unde:p - media patratica
- media cubica
k - ordinul ; k=2 pentru media patratica si k=3 pentru media cubica
k' - numarul de clase
ni - frecventa absoluta simpla
xi - centrul clasei de diametre
Mediile determinate pentru o colectivitate statistica omogena indeplinesc o conditia ca media patratica sa se afle intre media aritmetica si media cubica.
4.3. Determinarea medianei Me ( analitic si grafic )
Mediana reprezinta acea valoare care imparte sirul statistic sau seria de distributie in doua parti egale. Se calculeaza cu ajutorul formulei pentru valori grupate in clase:
Me = 42.5 (analitic) Me = 42,4( grafic )
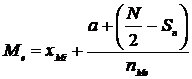
unde: Me - mediana
XMe - limita inferioare a clasei
a - amplitudinea clasei
N - volumul probei
Sn - frecventa absoluta cumulata pana la clasa imediat inferioare
clasei mediane
nMe - frecventa absoluta a clasei mediane in functie de N/2
Pe cale grafica mediana se determina pe graficul Ogiva frecventelor absolute cumulate. Frecventa absoluta cumulata a clasei mediane este punctul prin care se traseaza o paralela la abscisa graficului. Aceasta se prelungeste pana intersecteaza graficul. Din acest punct se coboara pe abscisa si se determina valoarea grafica a medianei.
Nr.crt
xi
ni
xi 
ni
ni
ni
ni
1
28
4
112
3136
87808
2458624
2
32
7
224
7168
229376
7340032
3
36
16
576
20736
746496
26873856
4
40
27
1080
43200
1728000
69120000
5
44
20
880
38720
1703680
74961920
6
48
21
1008
48384
2322432
111476736
7
52
16
832
43264
2249728
116985856
8
56
12
672
37632
2107392
118013952
9
60
5
300
18000
1080000
64800000
10
64
4
256
16384
1048576
67108864
11
68
2
136
9248
628864
42762752
Total
134
6076
285872
13932352
701902592
4.4. Determinarea modului ( analitic si grafic )
Modul reprezinta valoarea cu frecventa cea mai mare intr-o serie de distributie. Modul se determina pentru distributii unimodale, care au un singur maxim.
Mo = 43,64 ( analitic ) Mo = 43,3 ( grafic )
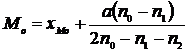
unde: XMo - limita inferioara a clasei modale
a - amplitudinea clasei
no - frecventa absoluta a clasei nodale
n1 - frecventa absoluta a clasei imediat inferioare celei nodale
n2 - frecventa absoluta a clasei imediat superioare celei nodale
Determinarea grafica a modului se face pe Histograma frecventelor absolute. In clasa modala, cu frecventa cea mai ridicata, se traseaza intersectia a doua segmente ce unesc limitele clasei cu limitele claselor alaturate. Din punctul de intersectie se coboara cu o paralela la ordonata pana la intersectia cu abscisa, determinandu-se astfel modul.
4.5. Interpretari
Media aritmetica, media
patratica, media cubica, mediana si modul sunt indicatori
statistici de pozitie care sintetizeaza informatiile referitoare
la zona catre care tind sa se centralizeze valorile experimentale.
Din calcul a rezultat ca valorile experimentale tind spre clasele
centrale. Deoarece relatia Mo=3Me-2 nu este valabila inseamna ca aceasta
serie de distributie este asimetrica. In acest caz este obligatoriu
ca valoarea medianei sa se afle intre valorile celorlalti doi
indicatori de pozitie, deci 
, conditie care este indeplinita.
5. Determinarea momentelor centrate de ordin 1 - 4 prin intermediul momentelor simple.
Momentele centrate sunt valori care folosesc pentru determinarea rapida a unor indici statistici. Pentru determinarea momentelor centrate este necesara determinarea momentelor simple. Calculul momentelor se face cu ajutorul formulelor pentru valori grupate in clase.
5.1. Calculul momentelor simple
m1 = 39,47 m2 = 417,75 m3 = 12836,48 m4 316326,16 7
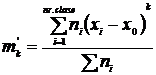
unde: mk - momentul simplu de ordin k
xi - valoare individuala
x0 - valoare de referinta
ni - frecventa absoluta simpla
In practica nu se alege o valoare de referinta arbitrara, ci se prefera utilizarea ca referinta a originii axelor de coordonate.
5.2. Determinarea momentelor centrate 
μ1=0
μ2=55,86
μ3=98,47
μ4=2474,36
6. Calculul indicilor de variatie ai distributiei empirice a diametrului de baza.
6.1. Determinarea amplitudinii de variatie
Amplitudinea de variatie reprezinta diferenta dintre valoarea maxima si valoarea minima din sirul statistic.
w = Xmax - Xmin, W = 28,0
6.2. Calculul variantei s2
Varianta sau dispersia reprezinta media patratelor abaterilor fata de media aritmetica. Unitatea de masura a variantei este patratul unitatii de masura a caracteristicii studiate. Aceasta se calculeaza cu ajutorul formulei pentru valori grupate in clase:
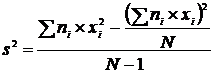s2 =47,41
unde: s2 - varianta
ni - frecventa absoluta simpla
xi - centrul clasei de diametru
N - numarul de unitati statistice analizate
6.3. Calculul abaterii standard s si al abaterii standard al mediei aritmetice sx
s = 6,88
Media aritmetica, determinata pentru un numar limitat de valori, prin calculul acesteia dorindu-se obtinerea unor informatii legate de populatia studiata, este insotita de o eroare numita abaterea standard a mediei aritmetice care se calculeaza cu formula:
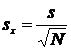sx = 0,58
unde: N - numarul de unitati statistice analizate
6.4. Calculul coeficientului de variatie
Coeficientul de variatie se calculeaza ca raport procentual intre abaterea standard si media aritmetica.
s % =17,44
6.5. Interpretari
La acest punct s-au calculat indicii de variatie. In cazul analizarii unei distributii experimentale trebuie sa se determine gradul de imprastiere a valorilor experimentale fata de valorile centrale. Aceasta masurare a imprastierii, a variatiei se rezolva prin determinarea si interpretarea indicilor de variatie. Dupa cum se observa, la aceasta distributie, s-a inregistrat o dispersie de 17,44%.
7. Determinarea indicilor de forma ai distributiei empirice a diametrului de baza
7.1. Indicele asimetriei A si eroarea acestuia sA
Pentru estimarea acestuia se compara media aritmetica cu modul si se observa ca distributia prezinta o asimetrie pozitiva sau de stanga. Acesta se calculeaza prin formule cum ar fi relatia lui PEARSON pentru distributii usor asimetrice sau relatia momentelor.
A
= 0,5042 A
= 0,2997
A = 0,2322
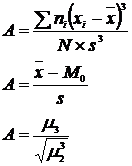
unde: ni - frecventa absoluta simpla
xi - centrul clasei de diametru
x - media aritmetica
N - numarul de unitati statistice
s - abaterea standard
μ - momente centrate corectate
Mo - modul
Este de asemenea insotit de o eroare.
sA = 0,4601
7.2. Indicele excesului E si eroarea acestuia sE
Excesul reprezinta deplasarea curbei
distributiei experimentale pe verticala in raport cu distributia
normala. Acesta se calculeaza prin doua formule si este
insotit de o eroare.
E = - 0,4375 E = - 0,4385 sE= 1,8299
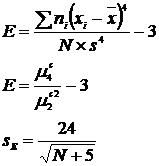
unde: ni - frecventa absoluta simpla
xi - centrul clasei de diametru
x - media aritmetica
N - numarul de unitati statistice
s - abaterea standard
- momente centrate
corectate
Tabel nr. 4
Nr.
crt.
xi
ni
xi - x
ni ( xi - x )3
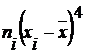
=39,47
1
28
4
-11.47
-6036.01
9233.08
2
32
7
-7.47
-2917.83
1796.18
3
36
18
-3.47
-752.075
609.699
4
40
29
0.53
4.317433
2.288239
5
44
20
4.53
1859.194
8422.147
6
48
21
8.53
1033.66
11177.1
7
52
17
12.53
3442.76
19037.8
8
56
12
16.53
1200.06
95927.1
9
60
5
20.53
1265.01
88230.7
10
64
4
24.53
1040.85
448272
11
68
2
28.53
444.61
325065
139
93.83
5484.6
518977
unde: xi - centrul clasei de diametru
ni - frecventa absoluta simpla
- media
aritmetica
7.3. Interpretari
Indicele asimetriei si excesului sunt indici de forma. Pentru estimarea indicelui asimetriei se compara media aritmetica cu modul. Deoarece media aritmetica este mai mica decat modul rezulta ca avem o asimetrie negativa sau de dreapta. Raportul dintre indicele asimetriei si abaterea sa este mai mic decat 2, deci distributia experimentala nu prezinta asimetrie semnificativa. De asemenea si raportul dintre exces si abaterea sa este mai mic decat 2, deci distributia nu prezinta un exces semnificativ.
8. Comparatie intre distributia experimentala si unele distributii teoretice
8.1. Ajustarea distributiei experimentale a diametrului de baza dupa legea distributiei teoretice normale.
Functia de distributie normala poate fi luata ca referinta pentru majoritatea proceselor care au loc in natura simultan printr-un numar mai mare de factori care actioneaza in mod egal. Ajustarea consta in inlocuirea unui set de experimentale cu un set de valori teoretice. Conditia pentru aplicarea acestui tip de ajustare este ca populatia sa fie omogena. Conditia pentru ca ajustarea sa se considere incheiata este sa existe egalitate intre volumul real si volumul obtinut prin insumarea frecventelor absolute teoretice. Ajustarea se face in mai multe etape:
- se determina abaterile normate ui pentru fiecare clasa formata in distributia experimentala;
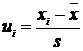
- se determina frecventele teoretice relative corespunzatoare functiei de distributie normale normate; aceste valori au fost luate din tabele.
- se determina frecventele absolute teoretice.
Tabel nr. 5
Nr. crt.
xi
ni
ui
f(ui)
-teoretic
rotunjit
1
28
4
2
32
7
3
36
18
4
40
29
5
44
20
6
48
21
7
52
17
8
56
12
9
60
5
10
64
4
11
68
2
139
unde: xi - centrul clasei de diametru
ni - frecventa absoluta simpla experimentala
- frecventa absoluta simpla teoretica
ui - variabila normala normata
f(ui) - functia de distributie normala
Verificarea grafica se face prin reprezentare. Ajustarea este corecta daca punctele experimentale sunt apropiate de curba teoretica.
Dupa aplicarea ajustarii trebuie sa se faca un test de ajustare.
8.2. Controlul normalitatii prin testul de ajustare
Tabel nr. 6
Xi
ni
rotunjit
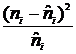
8
10
12
5
10
2,5
14
19
11
5,8181
16
14
16
0,25
18
27
22
1,1363
20
21
25
0,64
22
22
25
0,36
24
21
22
0,0454
26
17
16
0,0625
28
11
10
0,1
30
32
34
36
10
10
0
167
167
10,9123
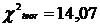
8.3. Folosirea distributiei teoretice CHARLIER de tip A pentru ajustarea distributiei experimentale a diametrelor de baza.
Folosind distributia CHARLIER de tip A, deci a derivatelor de ordin superior se poate obtine o distributie teoretica mai flexibila. Se observa ca aceasta ia in considerare indicele asimetriei si excesul. Pentru a ajusta distributiile experimentale cu ajutorul acesteia se porneste de la valorile determinate pentru frecventele relative teoretice ale functiei normale normate, iar valorile derivatelor se iau din tabele. Prin insumare rezulta frecventele relative dupa Charlier.
Tabel nr. 7
xi
ni
ui
f (ui)
f '''(ui)
f IV (ui)
φ (ui)
8
2
-2,483
0,0184
0,1439
-0,0723
-0,0055
0,0013
-0,0226
1,4417
1
10
0
-2,101
0,044
0,1302
-0,1765
-0,005
0,0033
0,0423
2,6985
3
12
3
-1,719
0,0925
-0,012
-0,5542
0,0004
0,0105
0,1034
6,5964
7
14
19
-1,337
0,1647
-0,2697
-0,7388
0,0104
0,014
0,1891
12,0637
12
16
14
-0,955
0,2541
-0,5062
-0,4067
0,0196
0,0077
0,2814
17,9521
18
18
27
-0,573
0,3391
-0,5171
0,3921
0,02
0,0074
0,3517
22,4369
22
20
21
-0,191
0,3918
-0,2206
1,0911
0,0085
0,0207
0,3796
23,9891
24
22
22
0,191
0,3918
0,2206
1,0911
-0,0085
0,0207
0,3626
22,9147
23
24
21
0,573
0,3391
0,5171
0,3921
-0,02
0,0074
0,3117
19,8851
20
26
17
0,955
0,2541
0,5062
-0,4067
-0,0196
0,0077
0,2422
15,4513
15
28
11
1,337
0,1647
0,2697
-0,7388
-0,0104
0,014
0,1683
10,7368
11
30
4
1,719
0,0925
0,012
-0,5542
-0,0004
0,0105
0,1026
6,5454
6
32
3
2,101
0,044
-0,1302
-0,1765
0,005
0,0033
0,0523
3,3365
3
34
2
2,483
0,0184
-0,1439
-0,0723
0,0055
0,0013
0,0252
1,6076
2
36
1
2,865
0,0067
-0,0989
0,1391
0,0038
0,0026
0,0079
0,5039
0
167
167
unde: xi - centrul clasei de diametru
ni - frecventa absoluta simpla experimentala
- frecventa
absoluta simpla teoretica
ui - variabila normala normata
f(ui) - functia normala normata
A - indicele asimetriei
E - excesul
(ui) - functia de frecventa
CHARLIER de tip A
8.4. Test de ajustare pentru distributia CHARLIER tip A.
Tabel nr. 8
xi
ni
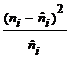
8
10
12
2
0
5
1
3
7
3,2727
14
19
12
4,0833
16
14
18
0,8888
18
27
22
1,1363
20
21
24
0,64
22
22
23
0,1666
24
21
20
0,05
26
17
15
0,2666
28
30
11
4
11
6
0,2352
32
34
36
3
2
1
3
2
0
0,2
Suma
167
167
10,9387
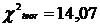
8.5. Reprezentari grafice si interpretari.
In urma compararii datelor
experimentale cu cele teoretice, respectiv cea a lui 
experimental, obtinut prin calcul, cu teoretic extras din tabele in functie de numarul de
grade de libertate f si procentul de transgresiune q, rezulta ca
distributia experimentala nu difera semnificativ de
distributia normala si de asemenea nu difera semnificativ
nici fata de cea CHARLIER de tipA..
f=k-m-1, unde: k - numarul de clase care s-au format dupa grupare
m- numarul de momente necesare determinarii valorii
functiei teoretice
Faptul ca punctele distributiei experimentale sunt apropiate de curba teoretica verifica rezultatul obtinut analitic.
