Corelatia

Corelatia

Corelatia masoara variatia concomitenta (covariatia) a doi factori. Nu masoara cauzalitatea.

Se noteaza r_xy = corelatia dintre variabilele x si y.

De fiecare dat se iau in calcul variabile perechi.

Exemplu:

Subiecti             Note matematica Note fizica x² y² xy

x y

A    7 7 49 49 49

B 9 8 81 64 72

C 10 9 100 81 90

D    6 7 36 49 42

E 9 10 81 100 90

F 8 7 64 49 56

G    5 6 25 36 30

H    3 4 9 16 12

I      7 6 49 36 42

J            8 7 64 79 56

K 6 7 36 49 42

L 7 7 49 49 49

M 6 6 36 36 36

N    5 6 25 36 30

n=14;          T1=96 T2=97 ax²=704;ay²=699; axy=696;

“Norul de puncte”

• daca este orientat spre dreapta - corelatie directa sau pozitiva (creste x, cretse si y);

• daca este orientat spre stanga - corelatie indirecta sau negativa (una creste, alta scade).

Coeficientul de corelatie variaza, indiferent de formula, intre –1 si 1. Cu cat este mai aproape de 1, cu atat corelatia este mai puternica. In jurul lui 0, relatia este de independenta.

1.     Coeficienti de corelatie

- se aplica asupra unor siruri de valori

a)      Coeficientul BRAVAIS – PIERSON (sau coeficientul de corelatie prin momentul produselor).

Formula de calcul este urmatoarea:

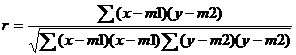
b)      Coeficientul biserial (intre o variabila continua si una dihotomica).

• N>50

Cote la test 0 1 2 3 4 5 6 7 8 9 10 Total

Rezultate

la examen

Admisi 0 1 0 3 5 10 16 11 6 3 159

Respinsi 1 2 4 7 13 22 9 4 2 0 054

Total                                1 3 4 10 18 32 25 15 8 3 1 113

Se calculeaza proportia celor admisi / respinsi.

p = P_admisi= q = P_respinsi=;

r_bis=,

unde: m1 = media valorilor x pentru elementele clasei superioare

(variabila continua);

m2 = media valorilor x pentru elementele clasei inferioare;

s = abaterea standard a intregii colectivitati;

pq / y = se citeste intr-un tabel special, in care se ia ca reper

fie p, fie q.

In exemplul nostru, ; s = 1.88;

Cu cat este mai semnificativ numarul subiectilor (mai mare), cu atat r_bis scade.

c)      Coeficientul de corelatie triserial

• avem aceeasi variabila continua, iar variabila discreta este trihotomica.

r_tris = ;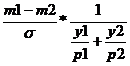

unde, m1 = mediile la testul X pentru cei buni;

m2 = mediile la testul X pentru cei slabi;

s = abaterea standard pentru intreaga populatie;

= proportia de buni;

= proportia de slabi.

d)      Coeficientul eneahoric

Exemplu:

Pentru stabilirea relatiei dintre inteligenta si timpul de reactie, s-au folosit doua probe, obtinandu-se urmatoarele rezultate:

y            Slabi Medii Buni

x

(7) (15) (3) D = 10

Buni n4 n1

Medii   (9) (14) (7)

Slabi     (5) n3 (12) (18) n2 C = 23

B = 12 A = 21

unde, A,B,C,D sunt totaluri pe orizontala si pe verticala, dar considerand numai colturile.

r =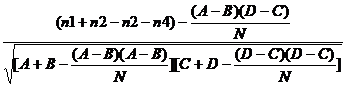

Daca A+B = C+D

A = B formula lui COUMETOU: r = 2g, unde

C = D g = ;

e)      Coeficientul de corelatie multipla ( R )

Se calculeaza atunci cand avem mai multi factori, ce concura la un anumit efect.

2.     Coeficienti neparametrici

a)     j - se aplica pentru doua distributii dihotomice.

Exemplu:

INITIATIVA

0 1

RAPIDITATE 1 30 50(c)

0 55 9

j = , unde a = (total ranul 1) / (total general)

b = (total coloana a doua) / (total general)

In exemplul nostru, T = 30+50+55+9=144;

a =

b =

c =

b)     Coeficientul de corelatie a rangurilor (Spearman)

r=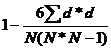

Exemplu: Clasificarea dupa frecventa controlului si calitate.

Subiecti             x y d d²

A 1 4 -3 9

B 2 2 0 0

C 3 10 -7 49

D 4 5 -1 1

E 5.5 1 4.5 20.25

F 5.5 3 2.5 6.25

G 7 8.5 -1.5 2.25

H 8 8.5 -0.5 0.25

I 9 7 2 4

J 10 6 4 16

r=0.36.            

Daca avem mai multi coeficienti de corelatie si vrem sa ne referim la aceasta colectie, se foloseste mediana.