
|
|
|
Calculul momentelor de inertie ale suprafetelor compuse
Calculul momentelor de inertie la pentru un domeniu material compus, cuprinde urmatoarele etape:
se descompune domeniul material intr-o serie de subdomenii simple;
se determina pozitia centrului de greutate al intregului domeniu material considerat, fata de un sistem de referinta arbitrar ales;
se calculeaza momentele de inertie axiale si momentul de inertie centrifugal in raport cu axele centrale, ale tuturor subdomeniilor materiale alese si care insumate, determina momentele de inertie ale intregului domeniu material considerat;
se determina pozitia axelor de inertie principale si valoarea momentelor principale de inertie.
Pentru exemplificare, se considera profilul din Figura 3.16 pentru care se parcurge algoritmul de calcul prezentat anterior.
se alege un sistem de referinta arbitrar O1y1z1;
se calculeaza pozitia centrului de masa in raport cu O1y1z1, corespunzator relatiilor
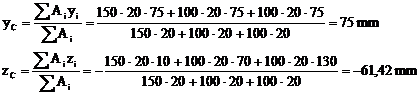

Fig. 3.16.
se calculeaza momentele de inertie in raport cu axele centrale Oy si Oz:
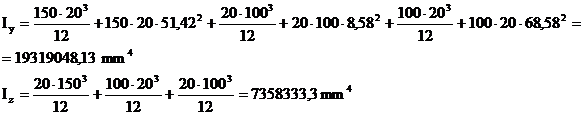
![]()
deoarece figura
prezinta simetrie, atunci ![]() si
si ![]() .
.
razele de inertie se calculeaza tinand seama de relatiile de definitie
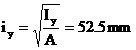
![]()
Observatia 3.9:
Calculul momentelor de inertie in raport cu un sistem de axe de coordonate legat de centrul de masa se poate face folosind relatiile de definitie.
Pentru bare, placi si corpuri avand forme mai mult sau mai putin regulate si care se folosesc frecvent in aplicatiile tehnice, relatiile de calcul sunt date in tabelul 3.3.
Tabelul 3.3. Momente de inertie
FIGURA SI SISTEMUL DE COORDONATE
Axa
MOMENTUL DE INERTIE
GEOMETRIC
MECANIC
Linia dreapta
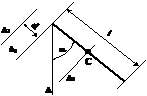
D2
![]()
![]()
D1
![]()
![]()
D
![]()
![]()
D3
![]()
![]()
Dreptunghi

O1x1
![]()
![]()
O1y1
![]()
![]()
Ox
![]()
![]()
Oy
![]()
![]()
Triunghi
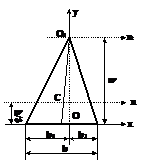
Ox
![]()
![]()
Cx1
![]()
![]()
O2x2
![]()
![]()
![]()
![]()
Tabelul 3.3: continuare
FIGURA SI SISTEMUL DE COORDONATE
Axa
MOMENTUL DE INERTIE
GEOMETRIC
MECANIC
Trapez isoscel
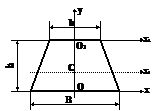
Ox
![]()
![]()
O2x2
![]()
![]()
Cx1
![]()
![]()
Oy
![]()
![]()
Cerc
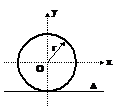
O
![]()
![]()
Ox
Oy
![]()
![]()
D
![]()
![]()
Coroana circulara
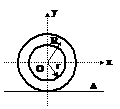
O
![]()
![]()
Ox
Oy
![]()
![]()
Elipsa
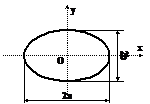
Ox
![]()
![]()
Oy
![]()
![]()
Sector circular
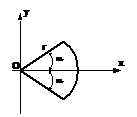
Ox
![]()
![]()
Oy
![]()
![]()
Segment de cerc
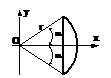
Ox
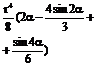
![]()
Oy
![]()
![]()
Tabelul 3.3: continuare
FIGURA SI SISTEMUL DE COORDONATE
Axa
MOMENTUL DE INERTIE
Paralelipiped
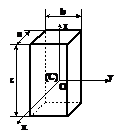
Ox
![]()
![]()
Oy
![]()
![]()
Oz
![]()
![]()
Cilindru
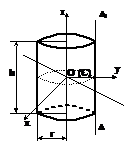
Oz
![]()
![]()
Ox
Oy
D
![]()
![]()
D1
![]()
![]()
Cilindru gol
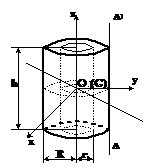
Oz
![]()
![]()
Ox
Oy
D
![]()
![]()
D1
![]()
![]()
Piramida dreptunghiulara
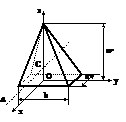
Oz
![]()
![]()
D
![]()
![]()
Ox
![]()
![]()
Con circular drept
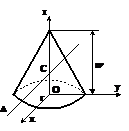
Oz
![]()
![]()
D
![]()
![]()
Tabelul 3.3: continuare
FIGURA SI SISTEMUL DE COORDONATE
Axa
MOMENTUL DE INERTIE
GEOMETRIC
MECANIC
Sfera
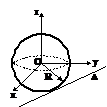
O
![]()
![]()
Oz
Ox
Oy
![]()
![]()
D
![]()
![]()
Sfera goala
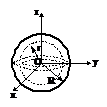
O
![]()
![]()
Oz
Ox
Oy
![]()
![]()
Sector sferic
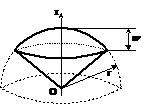
Oz
![]()
![]()
Segmentul de sfera
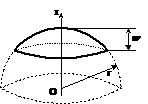
Oz
![]()
![]()