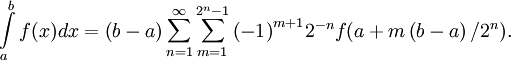Documente noi - cercetari, esee, comentariu, compunere, document
Documente categorii

Reguli pentru integrarea generala a functiilor

Informatii » scoala » matematica
biologiebotanicachimieculturadidacticadiversefilm fotografiefizicageografiegradinitainformaticaistoriematematicamuzicapsihicsport

Reguli pentru integrarea generala a functiilor

Pentru a real nenul:int af(x),dx = aint f(x),dx

int [f(x) + g(x)],dx = int f(x),dx + int g(x),dx



int f(x)g(x),dx = f(x)int g(x),dx - int left(int g(x),dxright),d(f(x))

Integrale ale functiilor simple

Functii rationale

mai multe integrale: Primitivele functiilor rationale

int 1,dx = x + C

int x,dx = frac + C

int x^n,dx = frac} + Cqquadmboxn ne -1

int frac,dx = ln + C

int } = arctan + C

Functii irationale

mai multe integrale: Primitivele functiilor irationale

int } = arcsin + C

int } = arccos + C

int } = mbox, + C

Functii logaritmice

mai multe integrale: Primitivele functiilor logaritmice

int ln ,dx = x ln - x + C

int log_b ,dx = xlog_b + xlog_b + C

Functii exponentiale

mai multe integrale: Primitivele functiilor exponentiale

int e^x,dx = e^x + C

int a^x,dx = frac} + C

Functii trigonometrice

mai multe integrale: Primitivele functiilor trigonometrice si Primitivele functiilor invers trigonometrice

int sin, dx = -cos + C

int cos, dx = sin + C

int tan , dx = -ln{left| cos right|} + C

int cot , dx = ln{left| sin right|} + C

int sec , dx = ln{left| sec + tanright|} + C

int csc , dx = -ln{left| csc + cotright|} + C

int sec^2 x , dx = tan x + C

int csc^2 x , dx = -cot x + C

int sec , tan , dx = sec + C

int csc , cot , dx = - csc + C

int sin^2 x , dx = frac(x - sin x cos x) + C

int cos^2 x , dx = frac(x + sin x cos x) + C

int sin^n x , dx = - frac cos } + frac int sin^ , dx

int cos^n x , dx = frac{cos^ sin } + frac int cos^ , dx

int arctan , dx = x , arctan - frac ln + C

Functii hiperbolice

mai multe integrale: Primitivele functiilor hiperbolice si Primitivele functiilor hiperbolice reciproce

int sinh x , dx = cosh x + C

int cosh x , dx = sinh x + C

int tanh x , dx = ln |cosh x| + C

int mbox,x , dx = lnleft| tanh right| + C

int mbox,x , dx = arctan(sinh x) + C

int coth x , dx = ln|sinh x| + C

Integrale definite care nu au primitive imediate

Exista cateva functii ale caror primitive (sau anti-derivate) nu pot fi exprimate intr-o forma fixa, imediat vizibila. Oricum, valoarea integralelor definite pe anumite intervale poate fi calculata. Unele dintre cel mai utile se gasesc mai jos.

int_0^infty{sqrt,e^,dx} = fracsqrt pi(a se vedea si Functia gamma - Gamma function)

int_0^infty,dx} = fracsqrt pi(Integrala lui Gauss - Gaussian integral)

int_0^infty{frac,dx} = frac(a se vedea si Numarul lui Bernoulli - Bernoulli number)

int_0^infty,dx} = frac

int_0^inftyfrac,dx=frac

int_0^infty x^,e^,dx = Gamma(z)(in care Γ(z) este Functia gamma - Gamma function)

int_^infty e^,dx=sqrt{frac}e^frac

int_^ e^ d theta = 2 pi I_(x)(in care I0(x) este Functia Bessel modificata de ordinul intai - Bessel function)

int_^ e^ d theta = 2 pi I_ left( sqrt right)

Metoda generalizata de aflare a primitivelor

Metoda urmatoare (in engleza, the method of exhaustion) da o formula pentru cazul general in care nu existe primitive imediate.

intlimits_a^b right)} sumlimits_^infty ^ right)^ } } 2^ f(a + mleft( right)/2^n ).


Copyright © 2023 - qgasesc.com. Toate drepturile pentru toate materialele apartin QGasesc.com.
Pentru detalii puteti sa ne contactati, politica de confidentialitate, termeni si conditii.