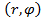|
|
|
Ecuatiile Lagrange
1. Ecuatiile Lagange de speta I
Lagrange obtine ecuatiile
care ii poarta numele din principiul lui D' Alambert prin exprimarea
desplasarilor virtuale
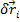
cu ajutorul coordonatelor generalizate
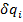. Cele doua tipuri de coordonate
sunt independente pentru legaturile olonome.
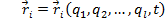
In acest caz, deplasarile virtuale
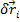,se mai scriu:
.
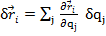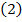
Cu ajutorul expresiilor
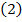, primul termen din expresia
principiului D' Alambert
se mai scrie:
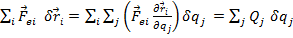
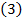
cu
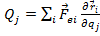, componentele fotelor generalizate.
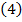
In general,
nu sunt lungimi (nu au dimensiunile unei
lungimi fizice) si
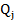nu sunt forte (nu au dimensiunile fortei)
dar,
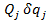este intotdeauna un lucru mecanic (o energie
transmisa catre ?? dinspre sistem).
Termenul al doilea din principiul D'Alambert se mai
scrie, inlocuind in
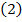
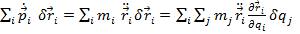
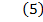
La randul sau
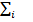se mai scrie:
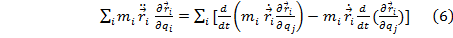
In continuare incercam sa introducem in
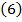viezele si derivatele acestora :
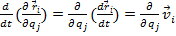
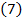
cu
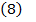
Derivata vitezei in raport cu vitezele generalizate este:
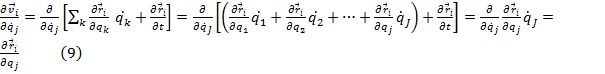
Inlocuind
in
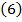, relatiile
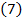si
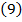, rezulta:
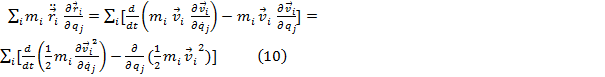
Daca
introducem o noua functie :
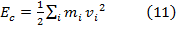
atunci
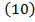devine :
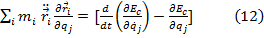
Inlocuind
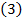si (
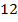)in principiul D'Alambert,
rezulta
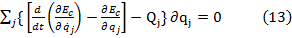
Pentru
legaturi olonome,
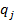fiind independenti,
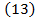este adevarata, daca coeficientii
deplasarii virtuale sunt nuli, adica:
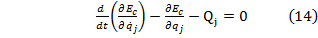
Ecuatiile
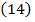poarta numele de ecuatiile lui Lagrange de speta I.
2. Ecuatiile Lagange de speta II
Daca
fortele aplicate
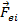sunt conservative, ele
deriva dintr-o functie potentiala numita, in general, energie
potentiala.
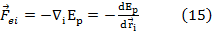
cu
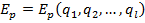, adica
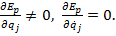
In acest caz, fortele generalizate
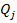se mai scriu:
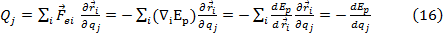
Daca
introducem functia lui Lagrange (langrageanul sistemului)
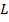, definit ca:
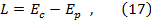
cu
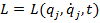, atunci ecuatiile lui
Lagrange capata forma:
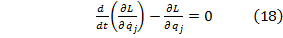
Sistemul de ecuatii
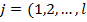) cu derivate partiale nu mai
contine fortele de legatura.
Aceste sisteme de ecuatii diferentiale
de ordin doi are
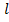functii necunoscute
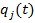. Solutiile sistemului vor
contine
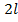constante arbitrare. Pentru a determina aceste
constante trebuie sa cunoastem conditiile initiale date
prin coordonatele generalizate si vitezele generalizate la momentul initial
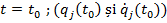
Proprietatile functiei Lagrange
a) Functia Lagrange a unui sistem format din subsistemele A si B care nu interactioneaza, este suma functiilor Lagrange a celor doua subsisteme (aditivitatea).
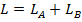
b)
Inmultirea functiei Lagrange cu o
constanta
nu modifica ecuatiile Lagrange
daca
, rezulta aceleasi
ecuatii Lagrange.
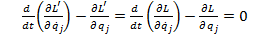
c)
Functia Lagrange este determinata pana
la derivata totala in raport cu timpul a unei functii
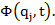
Daca
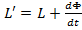,ecuatiile lui Langrange nu se
modifica.
Aplicatii:
1. Sa se scrie functia Lagrange pentr- un punct material, pentru un sistem de N puncte materiale libere si pentru N puncte materiale in interactiune.
Miscarea a doua corpuri care interactioneaza
prin campuri centrale (conservative)
Miscarea unui punct material in campul central generat de un alt corp,
considerat fix (Exemplu: miscarea in campul gravitational, miscarea in campul electrostatic).
Corp de
masa
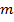, coordonate
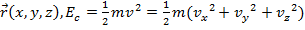si energie potentiala
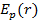
Pentru campul gravitational miscarea a fost studiata de Kepler (1609-1616) care a formulat trei "legi", prin prelucrarea datelor experimentale ale lui Tycho Brahe.
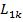. Miscarea este plana, pe orbite
eliptice cu sursa in focarul elipsei.
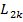. Viteza areolara este constanta
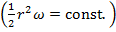
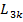
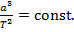
In coordonate
carteziene: trei coordonate si trei viteze
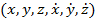
In coordonate
sferice:
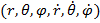
Deoarece miscarea
este plana
momentul fortei
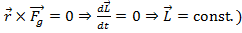aceasta reprezinta o constrangere
legatura
care reduce numarul de grade de libertate la 2
. Alegem coordonatele polare plane
