IMPRUMUTURI - Definitii si relatii de calcul, Imprumuturi cu anuitati constante, platibile la sfarsitul anului

IMPRUMUTURI

1. - Definitii si relatii de calcul

Se numeste imprumut operatia financiara prin care un partener numit creditor, plaseaza o suma de bani, pe o anumita perioada de timp,in anumite conditii unui alt partener numit debitor.

Operatiunea prin care debitorul restituie suma creditorului  se numeste rambursare sau amortizare a imprumutului.

Un imprumut care nu se mai inapoiaza se numeste imprumut nerambursabil.

Sumele rambursate anual care au rolul de a amortiza treptat suma imprumutata se numesc amortismente.

1. Amortizarea unui imprumut prin anuitati constante posticipate

Notatii:

- suma imprumutata la momentul initial

- anuitati (rate) succesive. Anuitatea se plateste la sfarsitul primului an.

- durata in ani a rambursarii

- amortismentele succesive continute in prima, a doua si a n-a anuitate

Tabelul de amortizare a unui imprumut prin anuitati constante posticipate se prezinta astfel:

Acest tabel este valabil pentru orice lege a anuitatilor pentru care nu s-a formulat nici o ipoteza privind plata acestora.

Ultima anuitate este egala cu ultimul amortisment la care se adauga dobanda corespunzatoare.

Relatia intre suma imprumutata si amortismente este:

Suma imprumutata este egala cu suma amortismentelor.

Relatia dintre anuitati si amortismente este:

2. Imprumuturi cu anuitati constante, platibile la sfarsitul anului

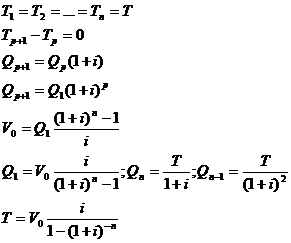
Calculul dobanzilor:

Calculul diferentelor dobanzilor:

Diferentele succesive ale dobanzilor formeaza o progresie geometrica crescatoare avand primul termen si ratia

Tabelul de amortizare a unui imprumut cu anuitati (rate) constante, platibile le sfarsitul anului (posticipat) se prezinta astfel:

Aplicatii

1.     Un imprumut de 10.000 u.m. urmeaza sa fie rambursat in 4 ani prin anuitati constante posticipate cu 5 . Sa se intocmeasca tabelul de amortizare.

2.     Un imprumut de 1000 RON urmeaza sa fie rambursat in 3 ani prin anuitati constante posticipate cu 6 . Sa se intocmeasca tabelul de amortizare.

3.     Un imprumut de 9000 urmeaza sa fie rambursat in 4 ani prin anuitati constante posticipate cu 8 . Sa se intocmeasca tabelul de amortizare.

3. Imprumuturi cu anuitati constante cu dobanda platita la inceputul anului

In conditiile in care se plateste la inceputul anului dobanda pentru primul an inseamna ca suma reala imprumutata este

Pentru fiecare din anii care urmeaza dobanda se calculeaza asupra sumei ramase de platit si se plateste odata cu amortismentul.

Tabelul de amortizare a unui imprumut cu anuitati (rate) constante cu dobanda platita la inceputul anului (anticipat) se prezinta astfel:

Deoarece , rezulta ca

Diferenta a doua anuitati succesive este:

Deoarece anuitatile sunt constante, se poate scrie:

obtinem

Suma imprumuturilor efectiv este egala cu suma amortismentelor. Rezulta ca:

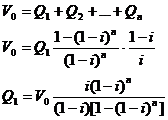
Aplicatii

1.     Un imprumut de 40.000 u.m. este rambursabil in cinci ani prin anuitati constante  cu dobanda platibila la inceputul anului cu procent de 5 . Sa se intocmeasca tabelul de amortizare.

2.     Un imprumut de 30.000 RON este rambursabil in patru ani prin anuitati constante cu dobanda platibila la inceputul anului cu procente de 6 . Sa se intocmeasca tabloul de amortizare.

3.     Un imprumut de 20.000 este rambursabil in trei ani prin anuitati constante cu dobanda platibila la inceputul anului cu procente de 4 . Sa se intocmeasca tabloul de amortizare.

4. Imprumuturi rambursabile o singura data

Pot exista doua cazuri:

Cazul I

Persoana sau institutia care a contractat imprumutul plateste anual dobanzile aferente sumei imprumutate urmand ca suma imprumutata sa fie platita dupa - n - ani la data expirarii contractului de imprumut impreuna cu dobanda ultimului an.

Daca dobanzile sunt calculate in conditiile unei dobanzi unitare - i - se poate scrie:

Anul 1:

Anul 2:

Anul n:

Acest mod de rambursare a unui imprumut este utilizat in situatiile in care suma nu are o valoare foarte mare.

Cazul II

Persoana sau institutia care a contractat imprumutul isi creeaza suma imprumutata prin depuneri periodice la o banca, timp de - n - ani pe baza dobanzilor unitare

Anuitatile fiind cunoscute se poate scrie:

Anul 1:

Anul 2:

Anul n:

Acest sistem de rambursare se numeste sistem american.

Suma care urmeaza sa fie rambursata dupa - n - ani se calculeaza cu relatia:

Pentru pregatirea acestei sume persoana sau institutia care a contractat imprumutul va depune la sfarsitul fiecarui an la o banca o anuitate constanta care se calculeaza cu relatiile:

Aplicatii

1.     O persoana imprumuta suma de 10.000 u.m. pe care urmeaza sa o ramburseze peste 5 ani impreuna cu dobanda calculata cu procent de 4%. Pentru a constitui aceasta suma persoana depune la sfarsitul fiecarui an o suma de bani cu procent de 5 . Care este suma pe care o depune?

2.     O institutie imprumuta suma de 20.000 RON pe care urmeaza sa o ramburseze peste 6 ani impreuna cu dobanda calculata cu procent de 5%. Pentru a constitui aceasta suma persoana depune la sfarsitul fiecarui an o suma da bani cu procent de 7 . Care este suma pe care o depune?

3.     O persoana imprumuta suma de 5000$ pe care urmeaza sa o ramburseze peste 3 ani impreuna cu dobanda calculata cu procent de 5%. Pentru a constitui aceasta suma persoana depune la sfarsitul fiecarui an o suma de bani cu procent de 6 . Care este suma pe care o depune

Imprumuturi cu amortismente egale

Amortismentele fiind egale se poate scrie relatia:

Dar,

Obtinem:

Anuitatile verifica relatia:

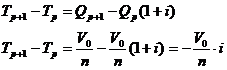
Obtinem:

Tabloul de amortizare a unui imprumut cu amortismente egale se prezinta astfel:

Aplicatii

1.     O persoana a imprumutat suma de 2000 u.m. pe care urmeaza sa o ramburseze in 4 ani cu procentul de 5 prin anuitati posticipate cu amortismente egale. Sa se intocmeasca tabloul de amortizare.

2.     O persoana a imprumutat suma de 30.000 RON pe care urmeaza sa o ramburseze in 3 ani cu procentul de 6% prin anuitati posticipate cu amortismente egale. Sa se intocmeasca tabloul de amortizare.

3.     O persoana a imprumutat suma de 40.000 pe care urmeaza sa o ramburseze in 4 ani cu procentul de 7% prin anuitati posticipate cu amortismente egale. Sa se intocmeasca tabloul de amortizare.