Metode de calcul a tensiunilor remanente la sudura

Metode de calcul a tensiunilor remanente la sudura

1.          Metoda de calcul a lui Nikolaev

Metoda este constituita pe ipotezele prezentate in capitolul 10.1.

Scopul metodei este determinarea parametrilor , b_n, y^* (figura 10.9) care permit construirea epurei deformatiilor plastice remanente  in sectiunea transversala a unei imbinari sudate cap la cap.

Pentru a determina parametrii indicati, trebuie studiate deformatiile longitudinale in sectiune transversala in doua faze: la incalzire si in stare remanenta dupa racirea totala. Sectiunea analizata nu conteaza deoarece se considera ca toate sectiunile transversale in sensul starii de deformare sunt identice. In ceea ce priveste stadiul de incalzire nu este de prea mare importanta care sectiune trebuie analizata. Nikolaev propune sa se analizeze deformatiile in sectiune transversala, unde la incalzire, in procesul de deplasare al sursei termice se atinge latimea maxima a izotermei de 600 C. La izoterma de 600 C se duc doua linii paralele tangente cu cordonul. Prin punctele de tangenta se duce sectiunea I-I (figura 10.9a).

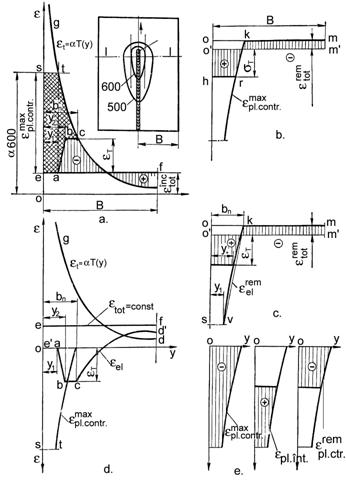
Figura 10.9. Epura deformatiilor longitudinale in sectiune longitudinala dupa Nikolaev.

In etapa de incalzire trebuie sa se analizeze sectiunea transversala in care latimea zonei deformatiilor plastice de contractie atinge o valoare mica. Acest lucru este posibil in sectiunea I-I. Totusi acest lucru nu este exact intocmai deoarece sursa termica se deplaseaza si temperatura va creste putin, lucru care va duce la cresterea latimii zonei deformatiilor plastice dar, nesemnificativa. Din acest motiv in sectiunea I-I se studiaza curba conventionala T_max(y) dusa la sectiunea data si nu cea reala. Metoda de calcul se bazeaza pe aceasta recomandare.

Daca curba temperaturii T_max(y) in sectiunea I-I este cunoscuta, atunci inseamna ca este cunoscuta in sectiunea data si curba deformatiilor termice  (figura 10.9a).

Deformatiile totale in stadiul de incalzire conform ipotezei sectiunilor plane, se vor determina printr-o linie orizontala. Compararea acestor doua deformatii in sectiune arata lipsa lor de corespondenta in afara de punctul lor de intersectie. Este evident ca fibrele longitudinale din apropierea marginilor laterale ale imbinarii au o deformare totala (observata, reala, cu modificarea formei), mai mare decat cea termica. Aceasta inseamna ca in imbinarea sudata aceste fibre sunt dilatate. Prin analogie este usor de explicat ca pentru fibrele amplasate in zona cea mai incalzita dincolo de punctul de intersectie al deformatiei termice si al deformatiei totale, va avea loc o compresiune elastica care se amplifica pe masura apropierii fibrei studiate de axa cordonului de sudura. In punctul c la distanta b_n de axa cordonului deformatiile elastice de compresiune ating nivelul limitei de curgere si raman asa pana in punctul b, aflat la distanta y₂ de axa cordonului si corespunde izotermei de 500 C. Pe distanta de la punctul b la punctul a deformatiile elastice de compresiune se reduc dupa o lege liniara conform diagramei e_T(T).

Punctul a este fata de axa cordonului la distanta y₁ corespunzatoare temperaturii de 600 C. Epura deformatiilor elastice echilibrate pe sectiune este reprezentata in desen cu hasururi drepte. In stanga punctului c, in fibrele longitudinale va fi nu numai o deformatie elastica ci si una plastica de compresiune. In stanga punctului a temperatura punctelor sectiunii este de 600 C si metalul in aceasta zona nu mai are proprietati elastice.

Pentru aceste puncte deformatia elastica este egala cu zero iar diferenta dintre deformatia termica si deformatia totala la incalzire va reprezenta deformatia plastica de contractie. Deformatiile plastice in sectiunea I-I sunt reprezentate in desen prin hasururi oblice.

Marimea deformatiilor plastice de contractie in desen este delimitata de o linie orizontala s-t, atat timp cat deformatiile plastice la temperatura mai mare de 600 C nu influenteaza formarea in imbinare a starii de tensiune. Componentele deformatiei totale in sectiunea I-I sunt reprezentate in figura 10.9b.

In continuare sunt prezentate formulele pentru componentele deformatiei totale, care sunt necesare in calculele ulterioare.

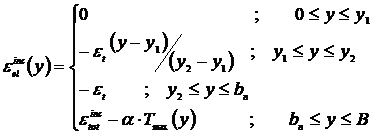
Pentru temperaturi maxime se pleaca de la formula cunoscuta a lui Rikalin

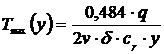(10.24)

unde: in [w];

• I, reprezinta curentul de sudare in A;
• u, tensiunea arcului in v; h, randamentul arcului;
• v, viteza de sudare in m/sec;
• d, grosimea pieselor sudate in m;
• c_g, caldura specifica volumica in J/(cm³ C);
• y, distanta de la axa cordonului pana la punctul dat in m.

Pentru atingerea scopului final (determinarea lui , b_n, y^*) trebuie ca in stadiul de incalzire sa se determine b_n si . Acesti doi parametrii se afla din urmatoarele doua conditii:

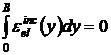
           (10.25)

Conditiile (10.25) se scriu sub forma dezvoltata:

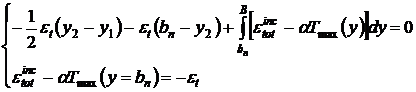       (10.26)

in care: ; ;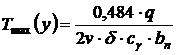

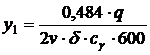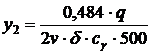
Rezolvand sistemul (10.26) se obtine:

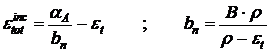     (10.27)

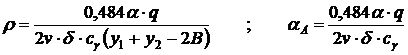       (10.28)

Deformatiile plastice de contractie in faza de incalzire in apropierea cordonului sunt mari si de aceea deformatia elastica de alungire care apare la racire in zona b_n atinge deformatia termica e_t. Pentru a satisface ipoteza sectiunilor plane trebuie ca fibrele centrale sa se alungeasca cu o anumita valoare (fig. 10.9d). Epura deformatiilor plastice remanente de contractie este data in aceeasi figura iar a celor elastice remanente in figura 10.9b.

Curba deformatiilor plastice remanente maxime,  este o functie complexa g, care nu este convenabila la integrarea urmatoare. De aceea curba svk o inlocuim cu o dreapta care este reprezentata in figura 10.9c. Eroarea in acest caz este nesemnificativa.

Pentru epura celelalte deformatii (deformatia remanenta elastica),  se pun urmatoarele conditii:

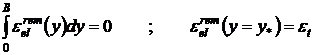                                   (10.29)

In diferite puncte pe sectiunea I-I deformatia elastica are expresia:

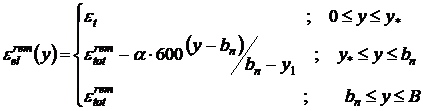       (10.30)

Tinand cont de (10.29) si conditiile (10.30) deformatiile se pot prezenta sub forma:

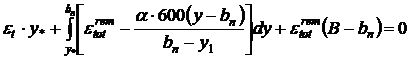
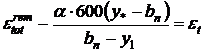                        (10.31)

Rezolvand sistemul (10.31) se obtin urmatoarele expresii:

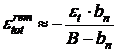               (10.32)

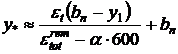                                (10.33)

Se definesc astfel doi parametrii care permit construirea epurei deformatiilor elastice longitudinale in sectiune transversala a imbinarii sudate.

Daca se studiaza un otel care nu este slab aliat, atunci in relatiile prezentate se inlocuiesc temperaturile de 500 si 600 C cu temperaturile corespunzatoare ale otelului considerat.

2.          Metoda de calcul a lui Trociun

In aceasta metoda sunt valabile toate ipotezele folosite de Nikolaev si in plus se presupune ca pe latimea zonei cu deformatii plastice 2b_n tensiunile remanente sunt repartizate uniform si egale cu limita de curgere a materialului s_c. Din aceasta ipoteza suplimentara trebuie ca in metoda de calcul a lui Trociun epura deformatiilor plastice remanente de contractie sa se ia nu sub forma de trapez din linii curbe ci sub forma unui dreptunghi asa cum este in figura 10.10.

Conditia de echilibru a fortelor interne longitudinale in sectiune transversala are forma:

                          (10.34)

unde: F_pl reprezinta suprafata sectiunii transversale a zonei cu deformatii plastice;

s_p reprezinta tensiunile longitudinale din afara zonei plastice;

F este suprafata sectiunii transversale a imbinarii.

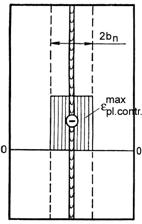
Figura 10.10. Epura deformatiilor plastice remanente dupa Trociun.

Conditia (10.34) se poate prezenta dupa deformatiile relative sub forma:

                             (10.35)

Din ecuatiile (10.34) si (10.35) rezulta parametrii de calcul a starii de deformare la tensiuni:

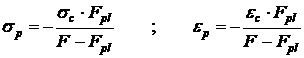                                   (10.36)

Prin urmare, pentru determinarea lui s_p sau e_p, trebuie sa se determine suprafata sectiunii transversale a zonei plastice F_pl. Daca latimea zonei plastice este 2b_n, iar grosimea placilor este d, atunci . Problema se reduce la determinarea dimensiunii b_n.

Primul mod de determinare al lui b_n

Dupa metoda lui Trociun b_n=b₁+b₂. Zona b₁ este limitata de temperatura T^* la care se pierd proprietatile elastice ale metalelor (pentru oteluri cu continut scazut de carbon 600 C; pentru aliaje pe baza de aluminiu 300 C; etc.). In zona b₂ la atingerea temperaturilor maxime, deformatia longitudinala totala a punctului analizat consta din deformatia termica, deformatia elastica si deformatia plastica. Deformatiile plastice de compresiune sunt conditionate aici mai ales de rigiditatea tablelor sudate. In zona b₁, in stadiul de incalzire, deformatiile elastice de compresiune nu se produc deoarece s-au transformat in deformatii plastice de acelasi semn.

Dimensiunea b₁ se poate determina din formula lui Rikalin pentru temperaturi maxime T_max in zona de langa cordon la distanta "y" de axa cordonului fara a considera pierderile la o cedare superficiala de caldura;

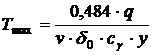     (10.37)

Daca prin "y" se intelege b₁, iar prin T_max temperatura T^*, atunci din (10.37) rezulta.

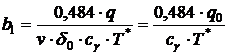                 (10.38)

unde d₀ este grosimea placilor sudate, sau suma grosimilor in care se raspandeste caldura de la sursa de incalzire, in cm;

v este viteza de sudare in cm / sec;

q este puterea sursei termice in w;

este energia specifica de incalzire in J/cm²;

c_g este capacitatea calorica volumetrica in J/cm³ C (Obs. Pentru oteluri c_g este 5,2, pentru aliaje de aluminiu 2,7 si pentru aliaje de titan 2,3).

Dimensiunea b₂ = f(h, s_T, q₀). La sudarea a doua placi cu latimea indicata h, dimensiunea b₂ = k₂(h-b₁). Daca se sudeaza placi cu grosime diferita, de exemplu in dreapta latimea placii b_dr, iar in stanga b_stg, atunci in placa vor fi latimi ale zonei cu deformatii plastice diferite:

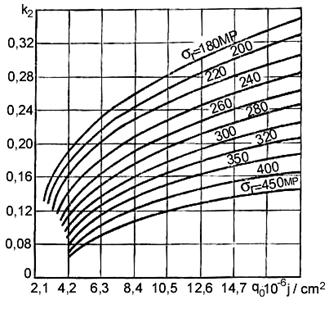
Figura 10.11. Coeficientul k₂ functie de q₀ dupa Trociun.

Pe masura cresterii lui h dimensiunea b₂ se modifica continuu. Saturarea se face (de exemplu) la h = 30 cm. Atunci cand h > 30 cm rezulta b₂= k₂(30-b₁). In cazul cordoanelor de colt sectiunea acestora se include in aria sectiunii zonei cu deformatii plastice. Coeficientul K₂ depinde de q₀ si se stabileste din graficul din figura 10.11 pentru punctul de curgere dat al materialului, s_c

Deoarece compozitia chimica a metalului si structura pentru diferite oteluri de constructie aproape ca nu influenteaza asupra repartizarii caldurii la incalzirea prin sudare, prin metoda reducerii si similitudinii se poate trece pur si simplu de la valorile k₂ pentru otelul de aceeasi marca la valorile  pentru otel de alta categorie cu ajutorul functiei:

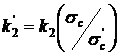              (10.39)

unde  reprezinta limita de curgere a otelului de alta categorie.

Al doilea mod de determinare al lui b_n

La baza acestei metode este formula pentru deformatii elastice de compresiune in zona de mijloc a placii cu crestaturi, la incalzirea ei in intervalul de temperaturi de la 0 la T₁. Astfel:

                                (10.40)

Deoarece:

, vom scrie relatia (10.39) sub forma:

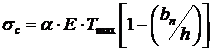                      (10.41)

Temperatura maxima pentru fibra pe distanta y, adica in cazul studiat b_n, tinand cont de pierderile de caldura prin radiatie, se defineste prin formula:

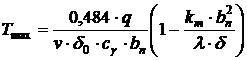            (10.42), unde: q este puterea efectiva a sursei de incalzire in J;

v este viteza de sudare in cm/sec;

d este grosimea data a placilor in cm;

c_g este caldura specifica in J/cm³ C;

b_n este semilatimea zonei cu deformatii plastice in cm;

k_m este coeficientul de degajare termica superficiala in J/cm² C;

l este conductibilitatea termica in J/cm C;

d este grosimea placii in cm.

Daca expresia din paranteza (relatia 10.42) care ia in consideratie pierderile prin cedare de caldura superficiala se noteaza prin "m" si se ia in consideratie ca , atunci ecuatia (10.42) se poate scrie sub forma mai scurta:

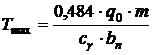     (10.43)

Rezolvand impreuna relatiile (10.41) si (10.42) functie de b_n, obtinem:

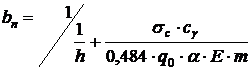          (10.44)

La sudarea otelurilor se recomanda ca pentru calculele practice sa se ia urmatoarele valori ale coeficientilor termofizici c_g=5,2 J/(cm³ C); k/l=0,008l/cm; a=12x10^-6 1/ C. Tinand cont de aceste valori si luand pe E=2x10⁷ MPa relatia (10.44) ia forma:

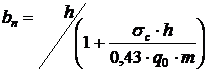                       (10.45)

unde  (b_n si d se iau in cm).

Pentru determinarea lui b_n in functie de (10.45) trebuie la inceput sa se ia m=0,6, sa se calculeze b_n, apoi dupa b_n dat sa se afle "m" si sa se compare cu "m" luat. Daca eroarea va fi semnificativa se ia o noua valoare a lui "m" si se repeta calculul. In cazul neglijarii pierderilor de caldura prin radiatie, "m"=1 si valoarea b_n se poate calcula cu relatia:

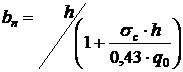                              (10.46)

Din datele lui Trociun diferenta dintre valorile lui b_n obtinute prin cele doua metode nu este atat de mare. La sudarea unor placi foarte mari (), formulele (10.45) si (10.46) se simplifica:

      (10.47)

             (10.48)