|
|
|
ANALIZA CINEMATICA A MECANISMELOR PLANE
1. Notiuni introductive
Analiza cinematica are ca scop studiul miscarii elementelor cinematice sau a unor puncte de pe ele, care pot fi chiar cuplele cinematice, fara a se studia fortele care provoaca miscarea.
Din analiza cinematica a mecanismelor rezulta parametrii cinematici, atat pentru elemente, cat si pentru punctele stabilite, in functie de miscarea si pozitia elementului conducator.
Acesti parametri cinematici sunt: pozitia elementului sau a punctului considerat; traiectoria descrisa de un anumit punct luat in studiu; viteza si acceleratia unghiulara a elementelor cinematice; viteza si acceleratia absoluta a punctelor considerate.
Acesti parametri cinematici se determina pentru un ciclu cinematic.
Analiza cinematica a mecanismelor poate fi realizata utilizand diverse metode.
Principalele metode utilizate sunt: metode grafice, metode grafo-analitice, dintre care cea mai cunoscuta este metoda poligoanelor de viteze si acceleratii; metode analitice, metode speciale, dintre care se pot mentiona metoda functiilor de transfer si metoda matriciala.
Asadar, sunt o serie de metode mai simple cu o precizie scazuta insa suficienta pentru scopul propus si metode mai complicate (metodele analitice sau cele speciale) cu o precizie foarte buna, atunci cand este absolut necesar, aceste metode realizandu-se cu succes, de regula, numai pe calculator.
In acest capitol se va realiza analiza cinematica a unor mecanisme utilizand metodele analitice si metodele speciale, celelalte metode (grafice, grafo-analitice) fiind prezentate doar cu titlu informativ. In literatura de specialitate sunt prezentate detalii in modul de aplicare a acestor metode pe diverse mecanisme intalnite in practica.[51];[62];[63];[70];[72];[87];[88].
2. Metodele grafice
Metodele grafice permit determinarea parametrilor cinematici, direct, prin constructii grafice, fara a se utiliza relatii de calcul intre parametrii determinati.
Precizia
la metodele grafice este mica si eroarea de estimare este de 
pentru traiectorii, 
pentru viteze, 
pentru
acceleratii.
Aceste precizii sunt totusi suficiente pentru unele analize, care pot fi realizate numai pentru puncte in miscare absoluta de rotatie sau de translatie.
Din randul metodelor grafice se pot enumera: metoda diagramelor, metoda centrului instantaneu de rotatie, metoda rabaterii.
Din randul acestor metode, mai interesanta este metoda diagramelor.
Aceasta metoda grafica, cunoscuta in literatura de specialitate sub denumirea de metoda derivarii grafice, se bazeaza pe faptul ca derivata unei functii este egala cu tangenta trigonometrica a unghiului format de sensul pozitiv al axei absciselor cu tangenta geometrica, dusa la curba functiei respective.[72].
In analiza cinematica a unui mecanism se porneste de la diagrama spatiului unui punct de pe elementul de lucru. De regula, se considera derivata in functie de pozitia unghiulara a elementului conducator. In aceste conditii, prin derivarea spatiului rezulta viteza redusa cu dimensiune liniara, respectiv acceleratia redusa, conform relatiilor urmatoare:
(1.18)
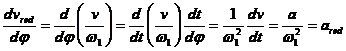(1.19)
Principiul metodei consta in determinarea, pe cale grafica, a unor corespondente intre marimile parametrilor cinematici si elementele mecanismului real, exprimate prin marimile reprezentative de pe desen cu ajutorul scarilor:
scara
lungimilor: 
scara
spatiului unghiular: 
scara
timpului 
scara
vitezelor 
scara
acceleratiilor 
Metoda grafo-analitica, cunoscuta si ca metoda ecuatiilor vectoriale, consta in rezolvarea grafica a ecuatiilor vectoriale, de tip Euler, pentru viteze si acceleratii cu aplicabilitate la elementele legate prin cuple de rotatie, de translatie de clasa cinci si prin cuple superioare de clasa patru. Metoda [62];[63];[72] prezinta unele avantaje:
precizie suficient de buna;
se poate aplica la toate punctele mobile ale mecanismului plan si la unele mecanisme spatiale;
sunt folosite calcule analitice simple.
Cu toate aceste avantaje, metoda are o serie de neajunsuri care, in ultimul timp, au facut ca ea sa fie mai putin utilizata desi din punct de vedere didactic conduce la formarea unei viziuni mai clare asupra modului cum actioneaza vitezele si in mod deosebit acceleratiile asupra mecanismelor. Dintre dezavantaje se mentioneaza:
volum mare de lucru;
nu poate fi utilizata la toate mecanismele.
Pentru rezolvarea parametrilor cinematici, prin aceasta metoda, se procedeaza astfel:
se stabilesc punctele pentru care se doreste analiza cinematica si pozitiile necesare ale elementului conducator;
se descompune mecanismul in grupe structurale;
se deseneaza mecanismul la scara, in toate pozitiile stabilite pentru elementul conducator tinandu-se cont de rezultatele unei, eventuale, analize pozitionale;
se scriu ecuatiile de tip Euler si se rezolva grafic la o scara aleasa in mod convenabil, care poate fi schimbata de la pozitie la pozitie si chiar la aceeasi pozitie la grupe diferite in functie de marimea vectorilor care trebuie desenati;
rezolvarea incepe cu elementul conducator si se termina cu ultima grupa introdusa la generarea mecanismului.
3. Analiza cinematica a mecanismelor prin metode analitice.
Utilizarea metodelor analitice, in analiza cinematicii mecanismelor, ofera o precizie ridicata si se poate aplica la o diversitate de mecanisme, atat plane cat si spatiale.
Pentru mecanismele simple, metodele analitice se aplica mai usor, in timp ce pentru mecanismele complicate, rezultatele se obtin mai greu. In unele cazuri, se obtin sisteme de ecuatii neliniare cu grade mai mari. In ultima perioada se utilizeaza calculatorul, cu programe adecvate, in rezolvarea acestor sisteme de ecuatii.
De regula, aceste metode, ca si metodele speciale, se aplica in laboratoarele de cercetare, unde tehnica de calcul este performanta si unde asemenea analize se fac in mod repetat pe structuri cinematice complicate.
Ca metode analitice utilizate, sunt: metoda numerica de rezolvare a ecuatiilor vectoriale si metoda contururilor vectoriale.
3.1. Rezolvarea numerica a ecuatiilor vectoriale.
Pentru transpunerea numerica a relatiilor vectoriale se precizeaza ca:
In cazul elementelor cinematice aflate in miscare de rotatie, viteza unui punct, de pe aceste elemente apare ca un determinant. In aceeasi situatie, acceleratia va fi descompusa in componenta normala (sub forma unei matrice coloana) si in componenta tangentiala (sub forma unui determinant). [62];[63];[72].
In cazul miscarii generale a punctului viteza si acceleratia apar ca o matrice coloana.
Se presupune ca a fost rezolvata configuratia mecanismului respectiv.
Se reaminteste ca o ecuatie vectoriala poate rezolva doua necunoscute scalare.
In ceea ce priveste notatiile utilizate, ele vor fi aratate pe parcursul analizelor cinematice a unor mecanisme ce vor fi luate ca exemple.
La primul exemplu de mecanism va fi urmarita o anumita succesiune de prezentare a metodei de rezolvare, urmand ca la celelalte exemple sa se utilizeze doar scrierea simbolica si dezvoltata a ecuatiilor, in vederea efectuarii calculului numeric, precizandu-se, de fiecare data, care sunt necunoscutele.
Mecanisme cu articulatii.
Exemplul 1
Fie mecanismul patrulater din figura 1.36.
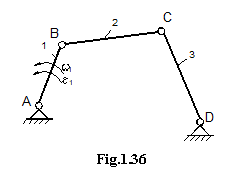
Viteze:
(1.20)
(1.21)
(1.22)
Ecuatiile scrise simbolic sunt:
(1.23)
(1.24)
(1.25)
Din ecuatia (1.23) rezulta:
, (1.26)
cu sistemul de ecuatii exprimat dezvoltat:
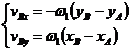(1.27)
de unde rezulta:
; (1.28)
Din ecuatiile (1.24) si (1.25) rezulta:
(1.29)
cu sistemul de ecuatii final:
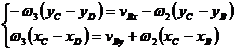(1.30)
rezulta ca necunoscute dupa
rezolvarea sistemului: 
si 
, si apoi din ecuatia (1.25) rezulta:
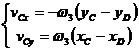(1.31)
si in final se obtine: 
.
In ecuatiile de mai sus s-au folosit [62];[63] urmatoarele notatii:
, 
, 
.
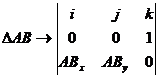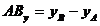Acceleratii:
Se parcurg urmatoarele etape:
(1.32)
(1.33)
(1.34)
(1.35)
Din ecuatiile (1.33) si (1.34 ):
(1.36)
Ecuatia (1.35) scrisa simbolic:
(1.37)
adica: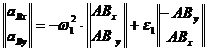 
(1.38)
Sistemul de ecuatii va fi:
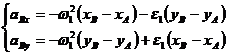(1.39)
de unde:
.
Ecuatiile (1.36) se pot exprima simbolic:
(1.40)
de unde:
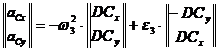
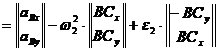(1.41)
Dezvoltat sistemul de ecuatii:
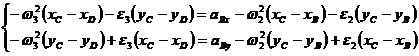(1.42)
vor rezulta 
; 
si apoi:
.
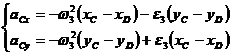Rezulta in final:
. (1.43)
Exemplul 2:
Fie mecanismul din fig. 1.37.
Viteze:
Ecuatiile scrise simbolic:
(1.44)
(1.45)
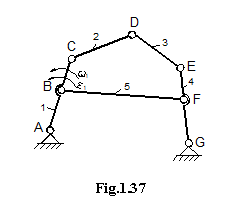
(1.46)
(1.47)
(1.48).
(1.49) 
(1.50)
Ecuatiile scrise dezvoltat:
Din ecuatia (1.44) rezulta:
(1.51)
cu dezvoltarea dupa sistemul:
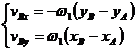(1.52)
de unde rezulta 
si 
iar in final se
obtine viteza punctului B ca
fiind:
.
Din ecuatiile (1.45) si (1.46) rezulta:
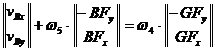(1.53)
de unde rezulta sistemul:
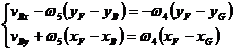(1.54)
Din sistemul (1.54) se vor obtine 
si 
.
Apoi din ecuatia (1.46) rezulta:
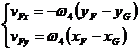
de unde se determina 
si 
.
In final rezulta: 
.
Ecuatia (1.47) devine:
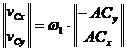(1.55)
cu forma dezvoltata:
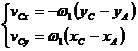(1.56)
Din sistemul (1.56) se vor determina 
si 
, pentru ca apoi sa se scrie:
.
Ecuatia (1.48) devine:
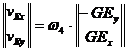(1.57)
de unde rezulta:
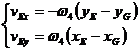(1.58)
Din sistemul (1.58) se vor determina 
si 
, pentru ca apoi sa se determine viteza punctului E:
.
Din ecuatiile (1.49) si (1.50) rezulta:
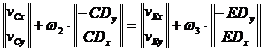(1.59)
de unde:
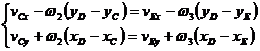(1.60)
sistem care are ca necunoscute si .
Din ecuatia (1.50) rezulta sistemul:
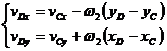
de unde se determina 
si 
pentru ca in final
sa se obtina:
.
Se observa din scrierea ecuatiilor ca s-a urmarit un anumit rationament in ordinea de rezolvare, pentru a se obtine doar sisteme de doua ecuatii cu doua necunoscute.
Dar rezolvarea poate fi facuta si global, atunci cand se utilizeaza programe de rezolvare pe calculator.
Acceleratii
Ecuatiile scrise simbolic:
(1.61)
(1.62)
(1.63)
(1.64)
(1.65)
(1.66)
(1.67)
Ecuatiile scrise dezvoltat:
Ecuatia (1.61) devine:
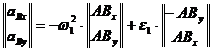(1.68)
de unde rezulta sistemul:
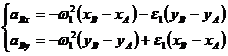(1.69)
Din rezolvarea sistemului (1.69)
rezulta 
si 
, pentru ca in final:
.
Din ecuatiile (1.62) si (1.63) rezulta:
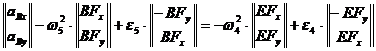(1.70)
cu dezvoltarea:
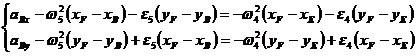(1.71)
Din rezolvarea sistemului de ecuatii (1.71)
vor rezulta: 
si 
.
In final din ecuatia (1.63) va rezulta:
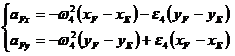
de unde se determina 
si 
, si in final: 
.
Din relatia (1.64):
(1.72)
de unde rezulta sistemul:
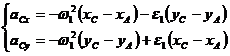(1.73)
Sistemul de
ecuatii (1.73) are ca necunoscute 
si 
.
In final va
rezulta: .
Relatia (1.65) se mai poate scrie sub forma:
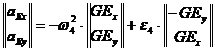(1.74)
de unde va rezulta:
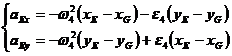(1.75)
Din rezolvarea sistemului (1.75) se vor
determina 
si 
, si in final: 
.
Din ecuatiile (1.66) si (1.67) se dezvolta scrierea:
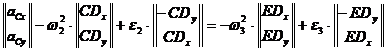(1.76)
de unde rezulta sistemul:
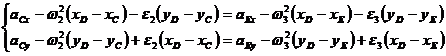(1.77)
Va rezulta, din sistemul de ecuatii
(1.77) ; , si apoi din relatia (1.66):
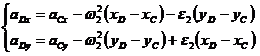
Se calculeaza 
si 
, si de aici: 
.
Mecanisme cu articulatii si culise.
Principii generale pentru calculul numeric.
Pentru fiecare problema de mecanisme cu articulatii si culise este bine sa fie sistematizat modul de rezolvare in urmatoarele etape:
1. Sa se precizeze punctul cu care trebuie inceputa rezolvarea. In mod obisnuit, pentru mecanismele mai simple, se obtin rezolvarile cele mai rapide, daca se incepe cu o articulatie.
2. Sa se stabileasca pe ce elemente se afla acest punct.
3. Sa se stabileasca care element este transportorul. De obicei se procedeaza prin eliminare.
4. Sa se scrie compunerea miscarilor conform ecuatiilor cunoscute din mecanica teoretica si anume:
(1.78)
, (1.79)
unde: 
- viteza de transport;
- viteza
relativa;
- viteza absoluta
a punctului B;
- acceleratia de
transport;
- acceleratia
relativa;
- acceleratia
Corriolis.
Este bine sa se utilizeze si alte notatii decat cele din mecanica teoretica, din care sa rezulte modul in care este privita miscarea de transport si miscarea relativa.
Astfel pentru
viteze: , se poate scrie: 
.
Pentru acceleratii: , se poate scrie: 
.
Exemplul 3
Fie exemplul de mecanism din figura 1.38.
Se observa ca:
se
incepe rezolvarea cu punctul B, care
apartine elementului 2 si,
bineinteles, si elementului 3.
transportorul, prin eliminare, este elementul 1.
Succesiv, se scriu ecuatiile:
vectorial: , cu scriere simbolica:
(1.80)
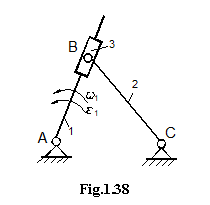
Expresia vitezei relative a avut la baza relatia vectoriala:
, cu 
.
Pentru acceleratii se procedeaza analog:
Vectorial:
(1.81)
Scriere simbolica:
(1.82)
Prin dezvoltarea ecuatiei (1.82)
si prin rezolvarea sistemului vor rezulta si 
.
Pentru scrierea acceleratiei relative s-a procedat ca la viteze, iar pentru acceleratia Corriolis, s-a utilizat exprimarea numerica a relatiei vectoriale:
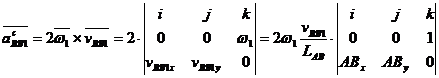
cu scrierea
simbolica: 
,
de unde
.
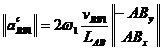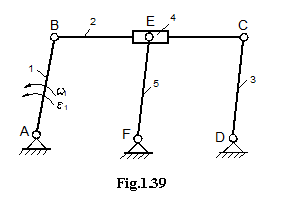Exemplul 4
Fie mecanismul din fig. 1.39.
Se vor scrie ecuatiile simbolice si dezvoltat pentru determinarea vitezelor si apoi se vor scrie si ecuatiile pentru determinarea acceleratiilor.
Determinarea vitezelor
Simbolic
(1.83)
(1.84)
(1.85)
(1.86)
Din ecuatia (1.86) rezulta:
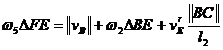(1.87)
Ecuatiile scrise dezvoltat:
Din ecuatia (1.83) se deduce forma:
(1.88)
de unde se dezvolta sistemul:
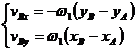(1.89)
va rezulta si iar in final se
obtine: .
Din relatiile (1.84) si (1.85) se obtine ecuatia:
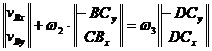(1.90)
Dezvoltat, va rezulta sistemul:
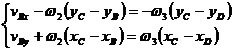(1.91)
prin rezolvarea caruia se vor
determina si .
Si apoi din ecuatia (1.84) va
rezulta si .
In final:
.
Ecuatia (1.87) se mai poate scrie si sub forma:
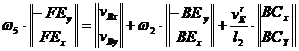(1.92)
cu dezvoltarea dupa sistemul:
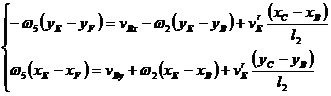(1.93)
prin rezolvarea caruia rezulta si 
.
Apoi:
.
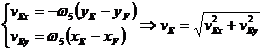Acceleratii
, (1.94)
, (1.95)
. (1.96)
.
(1.97)
(1.98)
(1.99)
(1.100)
. (1.101)
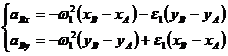(1.102)
Din rezolvarea sistemului (1.102)
rezulta: si , si in final:
.
Pentru acceleratia punctului C:
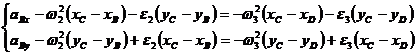(1.103)
Din rezolvarea sistemului de ecuatii (1.103)
vor rezulta: si .
In final din sistemul de ecuatii:
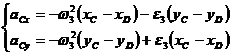
vor rezulta si , si in final: .
Pentru acceleratia punctului E:
Prin inlocuirea relatiilor (1.98), (1.99), (1.100) si (1.101) in relatia (1.97) se obtine sistemul de ecuatii:
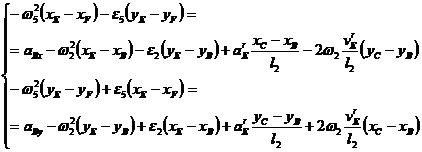
Din rezolvarea sistemului vor rezulta: si 
.
Apoi din sistemul:
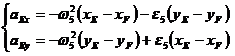
vor rezulta necunoscutele: si , si in final: .
3.2. Analiza cinematica a mecanismelor utilizand metoda
contururilor vectoriale.
Aceasta metoda se aplica pentru determinarea configuratiei si cinematicii mecanismelor complexe, unde metodele anterioare s-ar aplica cu mai multa dificultate.
Metoda contururilor vectoriale, are un caracter general si pentru inceput, ea va fi prezentata pentru doua cazuri simple de mecanisme plane: mecanismul patrulater, des intalnit in mecanica fina, si un mecanism cu culisa. [23];[62];[63];[72].
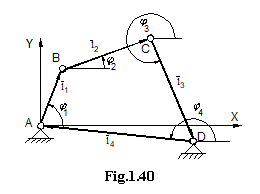
La
mecanismul patrulater din figura 1.40, se cunosc lungimile elementelor: 
; 
; 
; 
, 
, precum si miscarea elementului conducator: 
; 
si 
.
Prin analiza cinematica utilizand metoda respectiva, se pot urmari mai multi parametri cinematici din care cei mai importanti sunt: pozitia unghiulara a elementelor 2 si 3 fata de elementul fix 4; vitezele si acceleratiile unghiulare absolute ale elementelor; vitezele si acceleratiile unghiulare relative dintre elemente; vitezele si acceleratiile absolute ale unor puncte de pe mecanism, traiectoriile unor puncte.
Formandu-se din patrulaterul din figura, un contur vectorial, se scrie ecuatia vectoriala a conturului poligonal ABCD parcurs in sens orar:
(1.104)
Se proiecteaza ecuatia (1.104) pe axele sistemului fix, rezultand sistemul de ecuatii scalare:
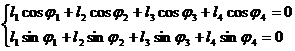(1.105)
Din
rezolvarea sistemului rezulta unghiurile 
si 
.
Pentru calculul vitezelor unghiulare absolute, se deriveaza ecuatiile scalare ale sistemului (1.105) si rezulta un nou sistem:
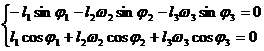, (1.106)
unde: 
; 
; 
.
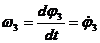Pentru
rezolvare, se apeleaza la un artificiu simplu, de a se roti sistemul de
axe fix cu unghiul , apoi cu , in sens pozitiv si se transcrie prima ecuatie a
sistemului (1.106) in noile sisteme, rezultand relatiile:
(1.107)
Considerand
ca 
se obtin vitezele
unghiulare:
(1.108)
(1.109)
Mecanismul patrulater se utilizeaza in mecanica fina, pentru transmiterea unui flux de semnale. Din acest motiv, se impune sa se determine raportul de transmitere dintre elementele de intrare (motor) si iesire (condus) - sensibilitatea s a semnalului. Valoarea acestui raport se calculeaza cu relatia (1.110):
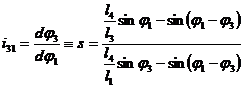(1.110)
Acceleratiile unghiulare absolute a elementelor conduse, se obtin derivand in raport cu timpul ecuatiile vitezelor unghiulare (1.108) si (1.109):
; 
.
Se deriveaza prima ecuatie a sistemului (1.106) rezultand ecuatia:
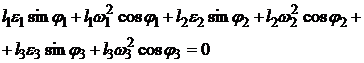(1.111)
Utilizand acelasi artificiu, de rotire a
sistemului fix cu si apoi cu si de transmitere
a ecuatiei (1.111) in noile sisteme, rezulta relatiile (1.112)
din care se deduc acceleratiile unghiulare absolute si .
Deci:
(1.112)
Apoi, prin rotirea sistemului fix cu :
.
Rezulta:
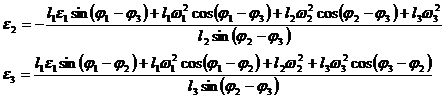(1.113)
Vitezele si acceleratiile unghiulare relative se determina cu relatiile urmatoare:
,
(1.114)
. (1.115)
Se
precizeaza ca vitezele si acceleratiile absolute se
introduc in relatiile de mai sus, cu semnele rezultate din calcul. Pentru
calculul vitezelor si acceleratiilor absolute ale unor puncte de pe
elementele cinematice ale mecanismului, se folosesc ecuatiile analitice
obtinute din transformarea ecuatiilor vectoriale.
[37];[62];[63];[72].
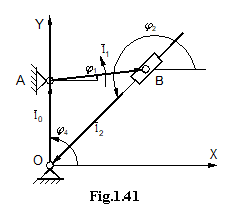
In
figura 1.41 este aratat un mecanism cu culisa, pentru care se cunosc:
, si miscarea
elementului conducator 1: , , .
Se poate scrie pentru conturul poligonal ecuatia vectoriala:
(1.116)
de unde proiectata pe axe:
(1.117)
Cele doua ecuatii scalare au ca
necunoscute si .
Derivand ecuatiile (1.117) in raport cu timpul se obtine:
(1.118)
Utilizand
acelasi artificiu simplu, prin rotirea axelor cu unghiul , vor rezulta necunoscutele si 
.
Pentru acceleratii se deriveaza ecuatiile precedente si se obtine:
(1.119)
, (1.120)
avand ca necunoscute si 
(si acum
relatiile pot fi decuplate).
In cazul in care structura mecanismului este complexa, este necesar sa se aplice procedeul proiectiilor conturului poligonal, pentru toate contururile inchise independente.
Numarul de contururi independente este dat de relatia:
, (1.121)
in care s-a notat cu c - numarul de cuple simple inferioare, in cazul in care toate elementele sunt constituite din bare.
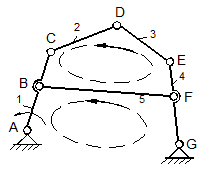
Fig.1.42
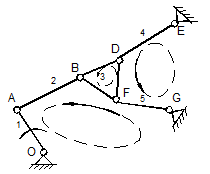
Fig.1.43
Astfel la mecanismul din figura 1.42 rezulta:
.
In cazul mecanismului din figura 1.43 rezulta:
.
Se poate verifica ca descompunerea in contururi inchise independente a fost efectuata corect, daca au fost incluse toate elementele, cel putin intr-un contur.
4. Metode speciale de rezolvare a cinematicii mecanismelor
Metodele speciale utilizeaza anumite functii sau matrici care conduc la determinarea vitezelor si acceleratiilor pe cai mai directe, cand metodele clasice sunt mai greu de utilizat.
In literatura de specialitate, se cunosc metode speciale, cele mai des intalnite sunt: metoda functiilor de transfer in cazul mecanismelor si metoda matriceala, de regula, in cazul robotilor sunt folosite mai mult.
4.1. Metoda functiilor de transfer
Se
defineste ca functie de transfer de ordinul unu, expresiile: 
; 
; . 
sau 
, respectiv, functiile de transfer de ordinul doi: 
; 
; . 
sau 
, in care 
sau 
sunt marimi
variabile, exprimate vectorial sau analitic, si pozitia
unghiulara a elementului conducator al unui mecanism. [72].
Cu aceste functii se obtin rapid vitezele necunoscute, cu urmatoarele relatii:
; . 
sau 
, (1.122)
respectiv acceleratiile:
; 
; .
sau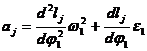 
. (1.123)
Se
poate constata imediat ca, utilizand metoda functiilor de transfer se
poate ajunge mult mai usor la vitezele si acceleratiile
elementelor necunoscute.
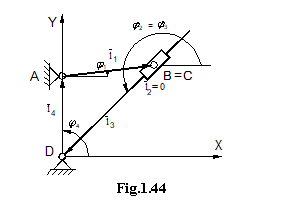
Pentru exemplificare, se considera mecanismul
culisa oscilanta, ABCD, din
fig. 1.44 pentru care se realizeaza partial, analiza cinematica
prin metoda analitica a contururilor vectoriale si prin metoda
functiilor de transfer pentru a sesiza mai bine diferentele
metodelor. Din analiza mecanismului se constata ca in conturul
vectorial atasat sunt doua necunoscute: si . [23];[72].
Ecuatia vectoriala a conturului si proiectiile ei pe axele sistemului sunt:
, unde 
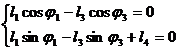(1.124)
de unde: 
; dupa derivare in raport cu timpul va rezulta
.
Separand
variabilele sistemului (1.124) si impartind a doua ecuatie
la prima, rezulta sub forma:
;
prin derivare rezulta.
Pentru obtinerea functiilor de transfer se deriveaza, fie ecuatia vectoriala (1.124), fie proiectiile sale pe axele sistemului, rezultand:
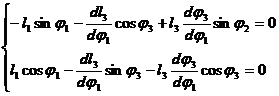(1.125)
Rotind sistemul cu unghiul si rescriind
relatiile in noul sistem, rezulta:
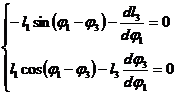(1.126)
de unde se deduc functiile de transfer de ordinul unu:
si 
(1.127)
Considerand expresia
analitica pentru si determinarea
vitezei cu ajutorul functiei de transfer, rezulta:
(1.128)
Daca
se face notatia 
si se
continua calculele, rezulta acceleratiile sub forma:
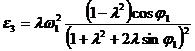
(1.129)
4.2. Metoda matriceala de rezolvare a cinematicii mecanismelor
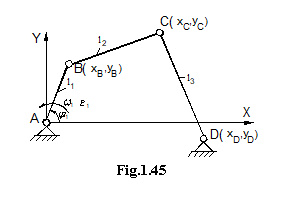Fie
mecanismul patrulater din figura 1.45.
Se vor determina viteza si acceleratia punctului C prin metoda matriceala, cunoscandu-se vitezele punctelor B si D, scrise matriceal astfel [23]:
; 
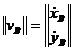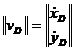(1.130)
Se cere sa se determine viteza punctului C, care este de forma:
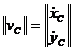. (1.131)
Vitezele de intrare 
si 
pot fi considerate ca
o marime matriceala de intrare, scrise sub forma:
.
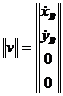(1.132)
Din conditia ca lungimile elementelor sa ramana aceleasi (adica sa fie nedeformabile) se pot scrie relatiile:
(1.133)
Pozitiile elementelor 2 si 3, fiind variabile in timp, se pot deriva relatiile (1.133) in raport cu timpul, obtinandu-se:
(1.134)
.
Sistemul de ecuatii (1.134) poate fi transcris matriceal astfel:
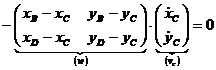. (1.135)
Aceasta scriere matriceala este valabila deoarece se bazeaza pe regula inmultirii matricelor (regula "inmultirii liniilor cu coloanele"). Rezulta atunci:
, (1.136)
de unde:
. (1.137)
Notandu-se prin
, (1.138)
unde 
este matricea de
transfer, se obtine:
,
iar 
este matricea vitezei
punctului C.
Derivandu-se ecuatiile (1.134) se obtine:
, (1.139)
care matriceal se va scrie sub forma:
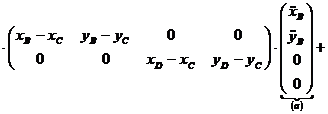
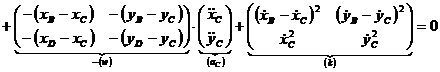(1.140)
sau
,
unde 
este matricea
acceleratiei punctului C.
