
|
|
|
POZITIILE RELATIVE A DOUA
DREPTE IN SPATIU. AXIOMA LUI
Definitie. Doua drepte situate in acelasi plan se numesc coplanare.
Definitie Doua drepte care nu au nici un punct comun si nu sunt paralele se numesc necoplanare.
Putem sintetiza pozitiile relative a doua drepte in spatiu.
i) Drepte coplanare:
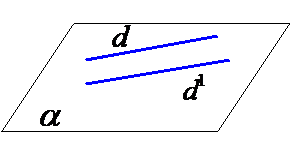 - paralele
- paralele 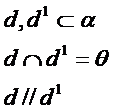
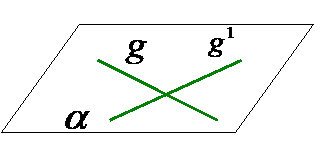
-concurente
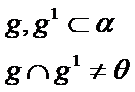
ii) Drepte necoplanare:
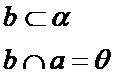
Exercitiu.Se da cubul ![]() Sa
se precizeze pozitia perechilor de drepte:
Sa
se precizeze pozitia perechilor de drepte:![]()
Axioma
lui
Printr-un punct exterior unei drepte se poate duce o paralela si numai una la dreapta data.
Tranzitivitatea relatiei de paralelism in spatiu.
In spatiu doua drepte distincte paralele cu o a treia sunt paralele intre ele.

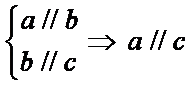
Exercitiu. Se da paralelipipedul ![]() Sa se precizeze pozitia relativa a
urmatoarelor perechi de drepte:
Sa se precizeze pozitia relativa a
urmatoarelor perechi de drepte:
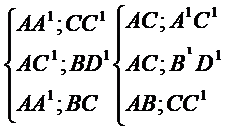
2. Unghiul a doua drepte in spatiu.
i) Unghiuri cu laturile paralele.
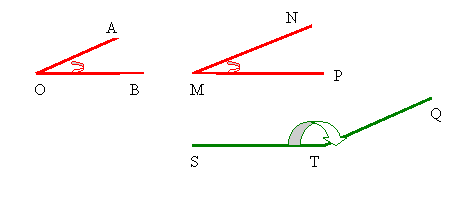
![]()
ii)
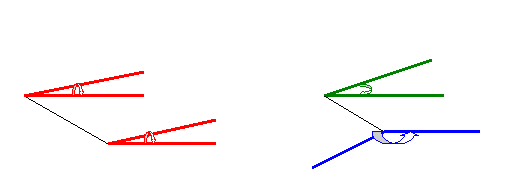
Unghiul a doua drepte in spatiu.
Definitie Prin unghiul a doua drepte in spatiu intelegem orice unghi ascutit sau drept cu varful in orice punct al apatiului si cu laturile paralele cu dreptele date.
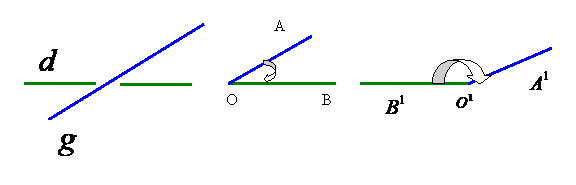
![]() necoplanare
Luam o un punct
necoplanare
Luam o un punct ![]()
oarecare
din spatiu ![]()
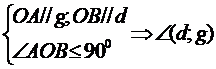
In ultima figura vedem cum nu trebuie construit unghiul a doua drepte in spatiu.
Observatii
De obicei varful unghiului se ia pe una din drepte.
Unghiul a doua drepte are
masura de ![]() daca si numai daca dreptele sunt paralele.
daca si numai daca dreptele sunt paralele.
Daca dreptele sunt concurente atunci ele formeaza un unghi plan.
 Exercitii.
Exercitii.
![]()
Sa se afle:
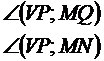
 In paralelipipedul alaturat sa se afle:
In paralelipipedul alaturat sa se afle:
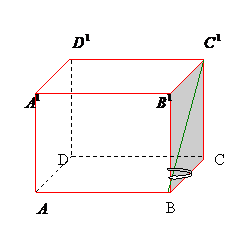
a)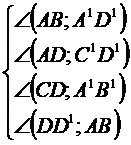
b) ![]() sa se calculeze:
sa se calculeze:
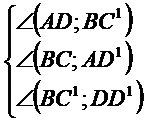
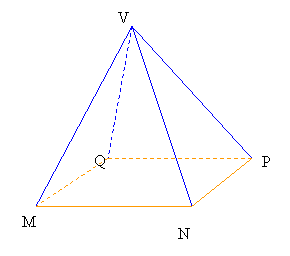
Se da o piramida
patrulatera VABCD cu varful in V iar O centrul bazei.Sa se determine unghiurile de mai jos stiind ca toate muchiile au lungimea a:
![]()
![]()
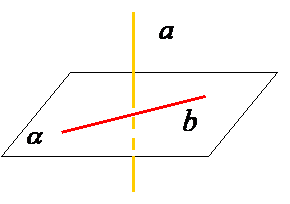
3.Pozitiile relative ale unei drepte fata de un plan, pozitiile relative a doua plane.

![]()
![]()
![]()
Dreapta este inclusa Dreapta este paralela Dreapta inteapa plan. cu planul. planul in A.
Teorema.
O dreapta paralela cu o dreapta din plan este paralela cu planul sau continuta in el.
Cu ajutorul acestei teoreme se poate stabili daca o dreapta este paralela cu un plan.
Exercitiu.
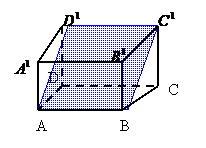 Sa se
stabileasca pozitia:
Sa se
stabileasca pozitia:
- dreptei
![]() fata de planul
fata de planul ![]() ;
;
- dreptei
![]() fata de planul
fata de planul ![]()
- dreptei
![]() fata de planul
fata de planul ![]()
Pozitiile relative a doua plane.
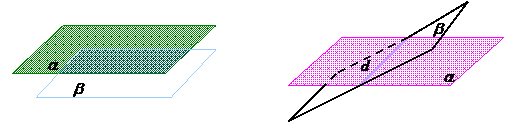
Plane paralele Plane secante
![]()
![]()
Exercitii.
i)
pozitiile dreptei ![]() fata de planele
fata de planele ![]()
ii)
pozitiile planului ![]() fata de planele
fata de planele ![]()
iii)
intersectia planelor ![]()
i)
M si N sunt mijloacele segmentelor![]()
ii) MA=4cm; MB=10cm; NA=6cm; Nc=9cm
iii) MA=4cm; AB=10cm; NC=10cm; AC=15cm