Calculul raspunsului unui sistem continuu linear invariant

Calculul raspunsului unui sistem continuu linear invariant

1. Calculul analitic. Ecuatia caracteristica

Ne intereseaza expresia analitica a raspunsului unui SLCI care reprezinta solutia ecuatiei sale diferentiale de transfer pentru o stare initiala precisa. Solutia generala y_g(t) a acestei ecuatii poate fi descompusa in doua solutii partiale:

1) solutia generala a ecuatiei diferentiale fara membrul drept;

2) o solutie particulara a ecuatiei diferentiale complete.

Cele n constante de integrare a functiei sunt determinate astfel incat solutia globala

satisface cele n conditii initiale.

Cum solutia generala este independenta de excitatia u(t), forma sa se obtine rezolvand ecuatia caracteristica asociata ecuatiei diferentiale de transfer:

. (2.15)

Am obtinut o ecuatie polinomiala care are n radacini r_k reale sau complexe (conjugate doua cate doua), distincte sau nu:

Cand radacinile sunt distincte, se obtine:

,

.

Daca toate radacinile nu sunt distincte, este suma celor n termeni obtinuti dupa cum urmeaza:

- fiecare radacina simpla r_j genereaza un termen:

.

- fiecare radacina dubla r_k genereaza doi termeni:

.

- fiecare radacina tripla genereaza trei termeni:

.

etc.

Remarca 2.1. : Raspunsul liber se obtine din solutia generala , determinand valorile care satisfac conditiile initiale x(t₀).

Exemplul 2.3. : Fie un SLCI a carui ecuatie diferentiala de transfer este:

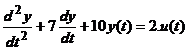
starea initiala fiind definita prin:

.

Dorim sa obtinem raspunsul sistemului la o treapta unitara:

.

Ecuatia caracteristica asociata ecuatiei diferentiale este:

,

avand ca radacini r₁ = -2 si r₂ = -5

Solutia generala a ecuatiei fara membrul drept este:

(2.16)

Deoarece o solutie particulara este furnizata de:

y_p(t)=0.2,

solutia generala se scrie:

(2.17)

Pentru a satisface starea initiala, trebuie sa alegem l₁ 2 si l₂ = -1, de unde rezulta ca:

Expresia (2.16) ne permite sa calculam raspunsul liber al sistemului care trebuie sa satisfaca aceleasi conditii initiale. Avem:

;

si deci raspunsul liber are expresia:

Pentru a calcula contributia regimului fortat la regimul relaxat, aplicam formula (2.17), dar in conditii initiale nule:

.

Obtinem constantele

si astfel:

Putem verifica principiul superpozitiei regimului liber si a regimului fortat:

In continuare se prezinta pe acelasi grafic curbele y₁(t), y_f(t) si y(t).

2. Integrala de convolutie

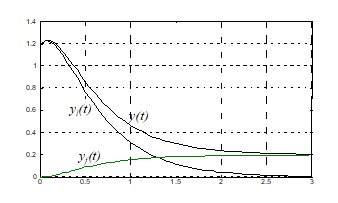
Raspunsul unui SLCI la un semnal de intrare oarecare poate fi obtinut plecand de la raspunsul sau la impuls

Fie s_D(t) raspunsul sistemului considerat la un impuls d_D(t) de arie unitate:

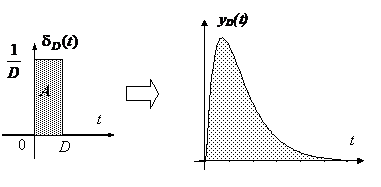
Sa consideram acum un impuls d_Dk(t) de aceeasi forma, dar intarziat cu k.D unitati de timp:

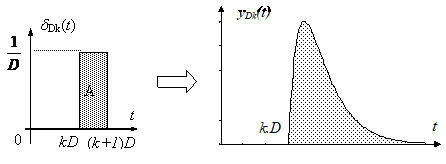
Deoarece sistemul considerat este invariant, raspunsul sau la semnalul de intrare s_Dk(t) va fi la fel, dar decalat cu k.D unitati de timp:

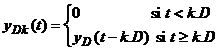
Fie u(t) un semnal de intrare cauzal oarecare. Putem determina raspunsul y(t) al sistemului considerat utilizand proprietatea de superpozitie. Pentru aceasta vom descompune u(t) conform schemei urmatoare:

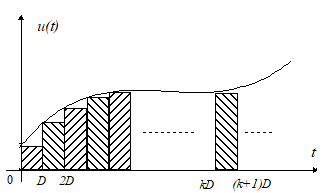
Intrarea u(t) poate fi astfel aproximata de o suma de impulsuri de largime fixa D si de inaltime egala cu u(t) pentru t = k.D, k=0, 1, .

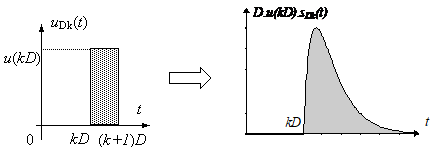
Fie u_Dk(t) impulsul care incepe la momentul k.D. Acesta poate fi exprimat in functie de impulsul intarziat d_Dk(t):

Tinand cont de linearitatea sistemului si de faptul ca s_Dk(t) este raspunsul la intrarea d_Dk(t), intrarea u_Dk(t) provoaca urmatorul raspuns:

.

La momentul t :

s-a aplicat al n+1-lea impuls, si deci:

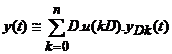
sau

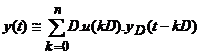(2.18)

Daca impunem ca D sa tinda spre 0, atunci

, (pentru ca t sa fie finit nenul)

si raspunsul y_D(t) tinde catre raspunsul impulsional:

Suma care constituie partea dreapta a ecuatiei (2.18) tinde catre o integrala definita.

Obtinem astfel:

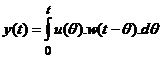(2.19)

Recunoastem in ecuatia (2.19) produsul de convolutie a doua semnale cauzale, care poate fi notat in forma:

y(t)=(u * w)(t)

Acest produs de convolutie poseda cateva proprietati prezentate in cele ce urmeaza.

Comutativitate:

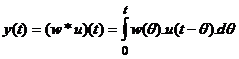(2.20)

Remarca 2.2. : Raspunsul impulsional (functia pondere) w(t) permite, prin intermediul ecuatiei (2.20), descrierea completa a comportamentului unui SLCI. Aceasta constituie un model neparametric al sistemului considerat.

Asociativitate

Fie trei SLCI conectate in serie, ca in figura urmatoare:

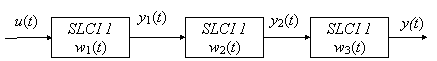
Avem:

y(t)=(w₃ * y₂)(t) , y₂(t)=(w₂ * y₁)(t) si y₁(t)=(w₁ * u)(t).

Semnalele u, w₁, y₁, w₂, y₂ fiind cauzale, obtinem:

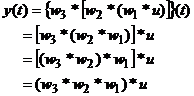
In final, putem scrie:

y(t)=(w * u)(t)

unde

Element neutru

Pentru semnalul de intrare d(t), raspunsul sistemului este functia pondere w(t). Se constata deci ca elementul neutru este impulsul unitar d(t):

.

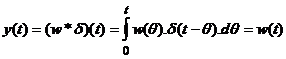In consecinta, obtinem:

(w * d)(t) = (d * w)(t) = w(t)