
|
|
|
PROIECT DIDACTIC
Clasa:a VIII-a
Disciplina: Matematica
Profesor mentor
Student practicant:
Unitatea de invatare:Proiectii ortogonale pe un plan
Subiectul:Reciprocele teoremei celor trei perpendiculare
Tipul lectiei: mixta: predare si consolidare
Timp de lucru:50 min
Locul de desfasurare:sala de clasa
Competente specifice:
Identificarea unor elemente ale figurilor geometrice plane in configuratii geometrice spatiale date
Interpretarea reprezentarilor geometrice si a unor informatii deduse din acestea, in corelatie cu determinarea unor lungimi de segmente si a unor masuri de unghiuri
Competente derivate:
C1. Enuntarea primei reciproce a teoremei celor trei perpendiculare;
C2. Demonstrarea primei reciproce a teoremei celor trei perpendiculare;
C3. Enuntarea celei de a doua reciproce a teoremei celor trei perpendiculare;
C4. Demonstrarea celei de a doua reciproce a teoremei celor trei perpendiculare;
C5.Calcularea distantei de la un punct la o dreapta;
C6. Calcularea distantei de la un punct la un plan.
Strategii didactice:
Metode: expunerea, explicatia, conversatia, exercitiul;
Mijloace de invatamant: manualul, culegerea, tabla, caietele elevilor, instrumentele geometrice;
Forme de organizare: individual, frontal.
BIBLIOGRAFIE:
Anton Negrila, Maria Negrila - Algebra Geometrie clasa a VIII-a , Bucuresti, Editura Paralela 45, 2003;
Mihaela Singer, Cristian Voica, Consuela Voica - "Matematica: manual pentru clasa a VIII - a"; Bucuresti; Editura SIGMA; 2000.
Ion Cuculescu, Constantin Ottescu, Olimpia Popescu -"Matematica: manual pentru clasa a VIII -a, Geometrie"; Bucuresti; Editura Didactica si Pedagogica;1997.
Anexe: Schema predarii, Fisa de lucru.
Momentele lectiei/timp
Competente derivate
Continutul lectiei
Strategia didactica
Activitatea profesorului
Activitatea elevilor
Metode si procedee
Mijloace de invatamant
Forme de organi-zare
Moment organizatoric
(2 minute)
Stabileste aspectele de disciplina si frecventa.
Verifica existenta resurselor materiale.
Raspund la intrebari
Conversatia
Frontala
Verificarea cunostintelor anterioare
(2 minute)
Profesorul verifica daca elevii si-au rezolvat tema si ii intreaba daca au intampinat dificultati in rezolvarea temei.
Raspund la intrebari
Conversatia
Manualul, Culegerea
Frontala
Anuntarea temei si a obiectivelor
(2 minute)
Profesorul anunta tema lectiei, obiectivele si noteaza titlul lectiei pe tabla.
Noteaza titlul lectiei in caiete
Explicatia
Tabla
Frontala
Predarea noilor cunostinte
(21 minute)

Fixarea cunostintelor
(21 minute)
C.1
C.2
C.3
C.4
C.5
C.6
Prima reciproca a teoremei celor trei perpendiculare:
Enunta teorema:
Daca dintr-un punct exterior unui plan ducem perpendiculara pe plan si perpendiculara pe o dreapta din plan, atunci dreapta ce uneste picioarele celor doua perpendiculare este perpendiculara pe dreapta data din plan.
Demonstreaza prima reciproca:
Se daAB, d , AC, Cd. Se cere BCd (Fig.1).
Dreapta d este perpendiculara pe planul triunghiului ABC pentru ca este perpendiculara pe doua drepte concurente din acest plan( pe AB si pe AC). Dar BC este continuta in planul triunghiului ABC. Rezulta ca dBC.
A doua reciproca a teoremei celor trei perpendiculare :
Daca intr-un punct al unei drepte dintr-un plan se duc doua drepte perpendiculare pe ea, prima exterioara planului si a doua continuta in plan, atunci perpendiculara dintr-un punct al primei drepte pe cea de-a doua este perpendiculara pe plan.
Demonstreaza cea de-a doua reciproca:
Se dau planul , punctul A si dreapta d,AC d, AC,
BC d, BC, ABBC. Se cere AB(Fig.2).
Dreapta AB este perpendiculara pe planul triunghiului ABC, fiind perpendiculara pe AC si si pe BC. Deci, este perpendiculara si pe AB, care este continuta in planul ABC, avand doua puncte(A si B) in acest plan. Deci ABd. Din ipoteza ABBC, deci AB(pentru ca contine atat pe BC cat si pe d , concurente in C).
Profesorul scrie pe tabla exercitiile din fisa de lucru .
Profesorul solicita prin sondaj elevii pentru a rezolva problemele din fisa de lucru.
Corecteaza si da indicatii acolo unde elevii gresesc sau au neclaritati
Elevii asculta si noteaza ceea ce profesorul explica. Pun intrebari in cazul in care e ceva ce nu inteleg.
Elevii ajuta la demonstrarea teoremei si pun intrebari in momentul in care nu inteleg
Elevii asculta si noteaza ceea ce profesorul explica. Pun intrebari in cazul in care e ceva ce nu inteleg.
Elevii ajuta la demonstrarea teoremei si pun intrebari in momentul in care nu inteleg
Elevii citesc problemele.
Elevii ies la tabla la indemnul profesorului pentru a rezolva problemele. Cei ramasi in banci rezolva problemele pe caiete.
1)Avand MA(ABC), construim MEBC, BC(ABC) ()AEBC. Construind triunghiul asa cum este el in realitate observam ca punctul E este pe prelungirea lui[BC] si deci desenul in spatiu il realizam pe prelungirea lui (CB.
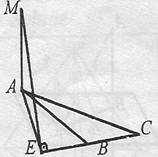
Pe
ME il calculam din triunghiul MAE m(![]() )=90
)=90![]()
![]() in care avem nevoie de AE. Analizand triunghiul ABC
gasim m(
in care avem nevoie de AE. Analizand triunghiul ABC
gasim m(![]() )=30
)=30![]() . In triunghiul BDC aplicamcos30
. In triunghiul BDC aplicamcos30![]() =
=![]()
![]() AC=4
AC=4![]() . In triunghiul AEC,m(
. In triunghiul AEC,m(![]() )=90
)=90![]() si m(
si m(![]() )=30
)=30![]()
![]() sin30
sin30![]() =
=![]() Deci in triunghiul MAE,
Deci in triunghiul MAE,
m(![]() )=90
)=90![]()
![]() (Teorema lui Pitagora) ME
(Teorema lui Pitagora) ME![]() =MA
=MA![]() +AE
+AE![]()
![]() ME=4
ME=4 ![]() d(M,BC)=4.
d(M,BC)=4.
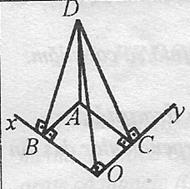
2)
Fie
DA![]() (XOY)
(XOY)![]() d(D,(XOY))=DA, pozitia acestui punct A nu o stim
momentan, dar rationand corect vom stabilo pozitia exacta a
sa.
d(D,(XOY))=DA, pozitia acestui punct A nu o stim
momentan, dar rationand corect vom stabilo pozitia exacta a
sa.
Notam:
d(D,OX)=DB si d(D,OY)=DC![]() DB
DB![]() OX; DB=6 si DC
OX; DB=6 si DC![]() OY, DC=3
OY, DC=3![]() . Din DA
. Din DA![]() (XOY), DB
(XOY), DB![]() OX, OX
OX, OX![]() (XOY)(
(XOY)(![]() )
)![]() AB
AB![]() OX (1).
OX (1).
Din
DA![]() (XOY),DC
(XOY),DC![]() OY, OY
OY, OY![]() (XOY)
(XOY)![]() (
(![]() ) AC
) AC![]() OY(2).
OY(2).
Din
(1) , (2) si unghiul XOYcu
masura de ![]()
![]() ABOC dreptunghi
ABOC dreptunghi![]() AC
AC![]() BO si AB
BO si AB![]() OC.
OC.
Din
triunghiul DBO, m(![]() )=90
)=90![]() avand DO=6
avand DO=6![]() si DB=6
si DB=6 ![]() (Teorema lui Pitagora)
(Teorema lui Pitagora)
DO![]() =DB
=DB![]() +BO
+BO![]()
![]() BO=6
BO=6![]() AC=6.
AC=6.
Din
triunghiul DAC, m(![]() )=90
)=90![]() avand DC=3
avand DC=3![]() si AC=6
si AC=6![]() ( Teorema lui Pitagora)
( Teorema lui Pitagora)
DC![]() =DA
=DA![]() +AC
+AC![]()
![]() DA=3
DA=3![]()
![]()
d(A,(XOY))=3![]()
Expunerea Explicatia
Explicatia
Exercitiul
Exercitiul
Explicatia
Manualul,
Tabla
Instrumen-tele geometrice,
Caietele elevilor
Fisa de lucru
Tabla
Caietele elevilor
Frontala
Indivi- duala
Frontala
Incheierea activitatii
(2 minute)
Da tema pentru ora viitoare
Noteaza tema in caiete
Explicatia
Culegere
Manual
Frontala
Schema predarii
Prima reciproca a teoremei celor trei perpendiculare:
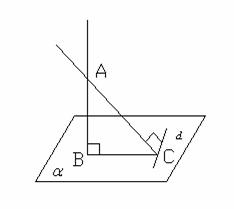 Daca dintr-un punct exterior unui plan ducem perpendiculara pe plan si
perpendiculara pe o dreapta din plan, atunci dreapta ce uneste
picioarele celor doua perpendiculare este perpendiculara pe dreapta
data din plan.
Daca dintr-un punct exterior unui plan ducem perpendiculara pe plan si
perpendiculara pe o dreapta din plan, atunci dreapta ce uneste
picioarele celor doua perpendiculare este perpendiculara pe dreapta
data din plan.
Demonstratie:
Fie A![]()
![]() , d
, d ![]()
![]() Fig.1
Fig.1
AB![]()
![]() , B
, B![]()
![]()
AC![]()
![]() , C
, C![]() d
d
![]()
![]()
![]() BC
BC![]() d
d
![]()
![]()
![]()
![]() A
A![]()
![]() AB
AB![]() d
d
AB![]()
![]()
![]()
![]() d
d![]() (ABC)
(ABC)
d![]()
![]() AC
AC![]()
![]() BC
BC![]() (ABC)
(ABC) ![]() d
d![]() BC
BC
A doua reciproca a teoremei celor trei perpendiculare :
Daca intr-un punct al unei drepte dintr-un plan se duc doua drepte perpendiculare pe ea, prima exterioara planului si a doua continuta in plan, atunci perpendiculara dintr-un punct al primei drepte pe cea de-a doua este perpendiculara pe plan.
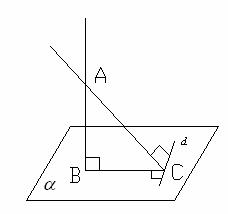 Fig.2
Fig.2
Demonstratie:
Fie planul ![]() , punctul A
, punctul A![]()
![]() si dreapta d
si dreapta d![]()
![]()
AC![]() d, AC
d, AC![]()
![]()
BC![]() d, BC
d, BC![]()
![]()
![]()
![]() AB
AB![]() BC
BC
![]() AB
AB![]()
![]()
![]()
![]()
![]() AC
AC![]() d
d
![]() BC
BC![]() d
d ![]() d
d![]() (ABC)
(ABC)
AB![]() (ABC)
(ABC) ![]() d
d![]() AB
AB
AB![]() BC
BC ![]() AB
AB![]()
![]()
BC![]()
![]()
d![]()
![]()
Fisa de lucru
Ex.1.
Fie triunghiul ABC isoscel
([AB]![]() [BC]) cu m(
[BC]) cu m(![]() )=
)=![]() . Pe planul sau ridicam perpendiculara MA, MA=2.
Daca BC=4, calculati d(M,BC)
. Pe planul sau ridicam perpendiculara MA, MA=2.
Daca BC=4, calculati d(M,BC)
Ex. 2.
Fie unghiul XOY cu masura
de ![]() si un punct D
exterior planului sau. Stiind ca: DO=6
si un punct D
exterior planului sau. Stiind ca: DO=6![]() , distanta de la D la OX este de 6, distanta de la
D la OY este de 3
, distanta de la D la OX este de 6, distanta de la
D la OY este de 3![]() , calculati distanta de la D la planul (XOY).
, calculati distanta de la D la planul (XOY).