practica la birotica profesionala

Stiinte Economice

Contabilitate si Informatica de Gestiune

PRACTICA LA BIROTICA PROFESIONALA

Problema 1

Sa se reconstituie traseul in calculator pentru operatia:

2663 ₁₀ + 1523 ₁₀ = 4186 ₁₀

Rezolvare

Transformand numarul 2663 din baza 10 in baza 8 obtinem:

2663 ₁₀ = 5147 ₈

Transformand 1523 din baza 10 in baza 8 obtinem:

1523 ₁₀ = 2763 ₈

Operatia va deveni in baza 8:

5147 ₈+ 2763 ₈ = 10132 ₈

Tabla de dunare in baza 8

Transformand numarul din baza 8 in baza 2 obtinem:

5147 ₈ = 101001100111

Si

2763 ₈ =10111110011

5147 ₈ + 2763 ₈ = 101001100111 + 10111110011 = 1000001011010

Numarul obtinut astfel in baza 2 devine , prin aplicarea algoritmului de tansformare a unui numar binar intr-un numar zecimal:

1000001011010 = 1*2¹² + 0*2¹¹ + 0*2 ¹⁰ + 0*2 ⁹+0*2 ⁸+ 0*2 ⁷+1*2 ⁶ +0*2 ⁵+ 1*2 ⁴+ 1*2 ³

+ 0*2 ² + 1*2¹ +0*2 ⁰ = 10132 ₈

1000001011010₂ = 10132 ₈ = 4186 ₁₀

Problema 2

Sa se reconstituie traseul in calculator pentru urmatoarea operatie :

75 ₁₀ x 13₁₀ = 975 ₁₀

Rezolvare:

a)     in baza 8

Transformam cele doua numere din baza 10 in baza 8:

Deci75 ₁₀ devine 113 ₈si 13 ₁₀ devine 15 _8.

Operatia din baza 10 devine in baza 8 :

113 ₈ x 15 ₈ = 1717 ₈

Verificare:

975 ₁₀ = 1717 ₈

Sau :

1717 ₈ = 1 x 8 ³ +7 x 8 ² +1 x 8¹ + 7 x 8 ⁰ = 512+(7 x 64) +8+ (7 x 1 ) = 975 ₁₀

b)     in baza 2

113 ₈ = 1001011

15 ₈ = 1101

Inmultind cele doua numere in baza 2:           1001011 x 1101=1111001111

11110011111 in baza 2 devine :

1*2⁹+1*2⁸+1*2⁷+1*2⁶+0*2⁵+0*2⁴+1*2³+1*2²+1*2¹+1*2⁰ = 512+256+128+64+0+0+8+4+2+1=975₁₀

Problema 3

Sa se intocmesca foaia de calcul ( in EXCEL ) pentru urmatoarea formula de calcul:

E

Rezolvare:

Tabela cu rezultate pentru expresia data este:

Varianta 1 s-a obtinut prin inlocuirea variabilelor a, b si c in expresia E (a,b,c) cu valorile din urmatoarea tabela de valori:

Variantele 2, 3,4 si respective varianta 5 s-au obtinut tinand cont de restrictiile impuse de existenta expresiei E (a,b,c):

a > 0, a < 0

b >0, b = 0

astfel:

VAR2 = IF ( a <>0, IF ( b>=0, E, "nu are sens radicalul"),"nu are sens impartirea)

VAR3 = IF ( AND(a <>0, b>=0), E, " nu are sens expresia")

VAR4 = IF ( AND(a <>0, b>=0),((4*a+c*b^1/2)/(2*a)), " nu are sens expresia")

VAR5 = IF ( AND(a <>0, b>=0), (4*a+c*(POWER(b,1/2)))/(2*a) , " nu are sens expresia")

Din foaia de calcul intocmita in EXCEL importam tabela cu formule aascunse , prin activarea optiunii FORMULAS din OPTIONS aflat in meniul TOOLS:

Problema 6

Sa se realizeze graficul de tip PIE pentru lista tipurilor de functii existente in meniul INSERT - FUNCTIONS din EXCEL

Rezolvare:

Apeland la optiunea FUNCTIONS pe care o avem in EXCEL in meniul INSERT alcatuim urmatorul tabel de variabile:

Pe baza datelor din tabelul de mai sus, in meniul INSERT optiune CHART selectam tipul de grafic pe care il dorim , cu posibilitati de selectare a pozitiei legendei ( stanga , dreapta, sus, jos) precum si a culorilor in care vrem reprezentarea grafica.

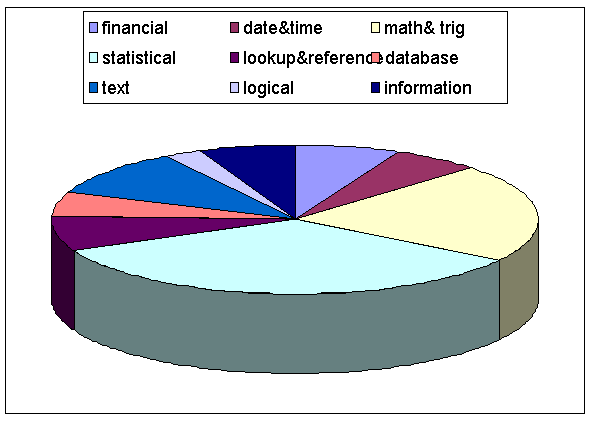
Problema 7

Sa se realizeze graficul de tip PIE pentru lista tipurilor de grafice existente in meniul INSERT - CHARTS din EXCEL.

Rezolvare :

Apeland la optiunea CHART pe care o avem in EXCEL in meniul INSERT alcatuim urmatorul tabel de variabile:

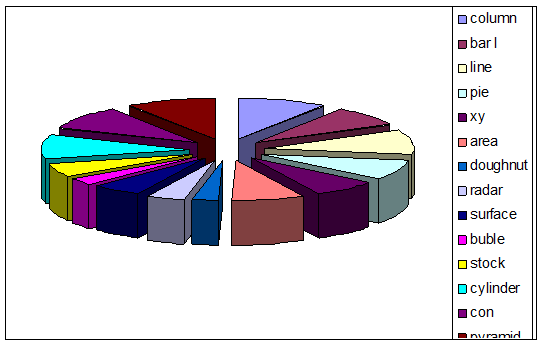
Problema 8.

Sa se determine dobanda capitalizata ( compusa ) pentru un imprumut de 35000 ron, cu o dobanda de 12% pe an obtinut pe o perioada de 6 ani si 3 luni.

Rezolvare

Dobanda capitalizata se obtine utilizand formula:

S = S ₀ * ( 1 + i ) ^t

Unde :

• t = timpul de plasament, exprimat intr-un numar intreg de perioade;
• S ₀= suma initiala;
• p = procentul;
• i p/100 = dobanda unitara;
• S = suma finala dupa un numar intreg de perioade.

Conform enuntului problemei:

S ₀ = 35000 ron

p = 12 %

t = 6 ani ,3 luni

i = p / 100

T = S ₀ * i /(1- u ^-t )]

u = 1+ i

Pentru datele problemei obtinem urmatoarea tabela cu rezultate ( tabela relizata in EXCEL):

Varianta 1 s-a obtinut prin inlocuirea variabilelor S₀, i si t in expresia S ( S₀,i,t ) cu valorile din enuntul problemei.

Varianta 2 s-a obtinut prin utilizarea functiilor finaciare din meniul INSERT - FUNCTION si selctand tipul de functie FINANCIAL.

In acest set de functii finaciare pentru fiecare variabila ( i, t, S_0, S,T ) exista o denumire prestabilita cu care opereaza aceste functii, astfel:

pentru i --- RATE

pentru t --- NPER

pentru S₀ ---PV

pentru S --- FV

pentru T---PMT

Cu ajutorul acestor functii financiare s-au obtinut variantele 2 si respectiv 3. Din EXCEL importam tabela de formule ascunse:

Problema 9

O societate comerciala detine in depozitul sau de marfuri urmatoarele 11 produse cuprinse in tabelul de mai jos. Cunoscandu-se stocul initial si pretul unitar pentru fiecare produs in parte , precum si intrarile si iesirile de marfa din ziua respectiva sa se intocmeasca inventarul marfurilor din depozit la sfarsitul zilei ( balanta analitica)

Rezolvare :

Stocul final (buc) = Stoc initial + Intrari - Iesiri

Pret total = Pret unitar( PU) * Stoc final

Din EXCEL importam tabela cu formule ascunse pentru a putea vedea formulele utilizate pentru calculul stocului final pe fiecare produs atat cantitativ cat si valoric

Pentru a putea vizualiza mai sugestiv stocul disponibil s-a realizat urmatorul grafic:

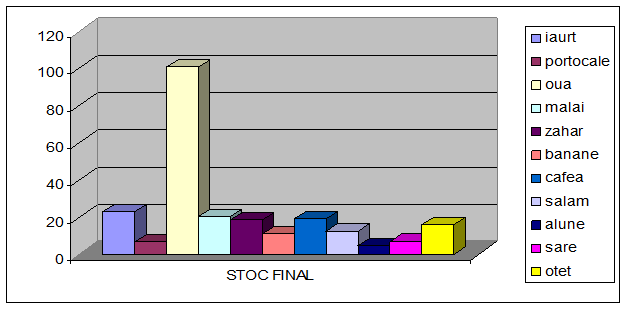
Problema 10

Pentru fiecare din cei patru salariati ai SC BIROTICA SRL sa se stabileasca venitul impozabil si apoi salariul net, cunoscandu-se urmatoarele date:

salariul brut - SB

somaj angajat = 1% *SB

sanatate angajat = 6,5%*SB

CAS (pensie) = 9,5%* SB

Rezolvare:

Venitul impozabil ( VI) pentru fiecare salariat se obtine prin scaderea tuturor retinerilor de mai sus din salariul brut:

Tabela de valori obtinuta in EXCEL, pentru verificarea rezultatelor este:

Unde am calculat separate cele 3 procente: 1%, 6,5%, 9,5%

Problema 11

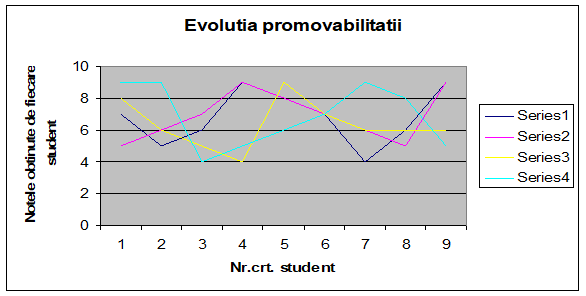
Sa se reprezinte grafic situatia la examenul de licenta a studentilor grupei AM CIG, avand la dispozitie notele obtinute de acestia la cele 4 materii de licenta.

Rezolvare:

Utilizand datele existente se alcatuieste lista studentilor participanti la examenul de licenta:

Media notelor obtinute penrtu fiecare student s-a obtinut astfel:

Media notelor = (Nota materia 1+ Nota materia 2+ Nota materia 3+ Nota materia 4) / 4

Aceleasi rezultate le obtinem mult mai simplu utilizand o foaie de calcul in EXCEL:

Pentru obtinerea acestor rezultate s-a utilizat functiile logice IF, AND, si AVERAGE disponibile in meniul INSERT - FUNCTION- LOGICAL.

Vizualizam aceste functii prin importul tabelei de valori din EXCEL de mai jos.

Pe aceeasi foaie de calcul s-a calculat functia logica AND

Pentru a ilustra grafic evolutia promovabilitatii studentilor actionam pictograma CHART, selctam tabelul cu notele obtinute de studenti la examene

Problema 12

Vanzarile unui magazin de bijuterii pe primele zece luni ale anului 2006 au urmatoarea evolutie:

Sa se stabileasca functia de ajustare si sa se prognozeze vanzarile magazinului pe urmatoarele 5 luni.

Rezolvare:

Observam ca vanzarile magazinului urmeaza o lege liniara de forma:

Y = a ₀+ a ₁* x

Pentru rezolvare codificam luna cu x _isi volumul vanzarilor (mil.lei) cu y _i.

Cautam o functie f(x) = y, aplicand metoda celor mai mici patrate obtinem sistemul:

10* a ₀ + 120* a ₁ = 126

120* a ₀ + 385* a ₁ = 863

Cu solutia obtinuta prim metoda eliminarii complete: a ₀ = 1.27 si a ₁ = 2.06.

Deci avem functia: Y = 1,27 + 2,06* x

Pentru a rezolva problema economica , utilizam o foaie de calcul din EXCEL:

Estimarile obtinute pentru urmatoarele 5 luni sunt redactate in culoare diferita.

S-au utilizat functiile din EXCEL - INTERCEPT si SLOPE existente in meniul Function.

Pentru vizualizarea utilizarii lor importam tabela de valori din Excel.( meniul TOOLS - Options- Formulas)

Reprezentand grafic rezultatele obtinem urmatorul grafic

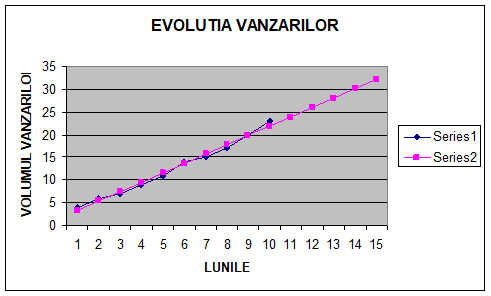
Problema nr. 13

Sa se rezolve urmatoarea problema de optimizare:

2*x +y ≤ 5

x+2*y ≤ 4

x, y, ≥ 0

(max)f=7*x+8*y

Rezolvare:

Utilizand algoritmul simplex gasim solutia: x = 2 si y = 1

Deci (max) f = 22

Aceasta problema se poate rezolva si prin solutie obtinuta cu ajutorul programului EXCEL urmarind urmitoarele etape:

alcatuim foaia de calcul in Excel

A           B C D E

importam din excel foaia de calcul cu formule , utilizand din meniul Tools - Options optiunea Formulas:

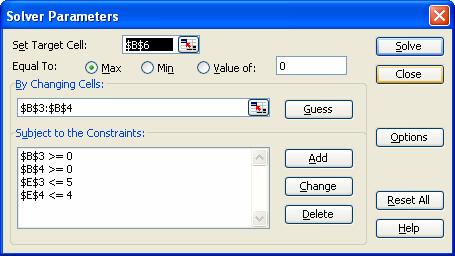
Tot in meniul TOOLS gasim functia SOLVER cu care obtinem max functiei f' = 22, introducand pe rand restrictiile date