|
|
|
Energia potentiala de deformatie
Energia potentiala de deformatie a unui corp se calculeaza cu:
W=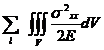 
.Pentru cazurile particulare de solicitare
la intindere respectiv compresiune, se obtine o anumita expresie de
calcul a energiei potentiale de deformatie avem: 
; dV=A(x).dx W= =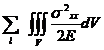
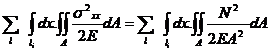; unde ( V) este volumul barei supusa la
solicitarea de intindere sau compresiune
L = W=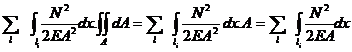 
; N=N(x);
A= A(x). Pentru cazul particular, unde N(x)= N = ct si
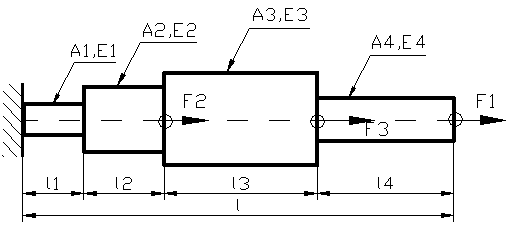
Figura 70
A(x)=A=ct. sunt constante ,
W=
dar cum dl= 
;
L = W= 
1. Teoremele lui Castigliano
Fie un corp elastic asupra
caruia actioneaza un sistem de forte concentrate F1 ,
F2 , F3, ., Fk , Fp in
echilibru, aici se aplica principiul suprapunerii efectelor. Cand
actioneaza sistemul de forte asupra corpului (C) din figura 71
, corpul se deformeaza si inmagazineaza o energie
potentiala de deformatie L , egala cu: 
.
Daca una din forte , anume Fk,
se mareste cu dFk , atunci creste si energia
potentiala de deformatie cu 
si energia
totala va fi:
L + ( a )
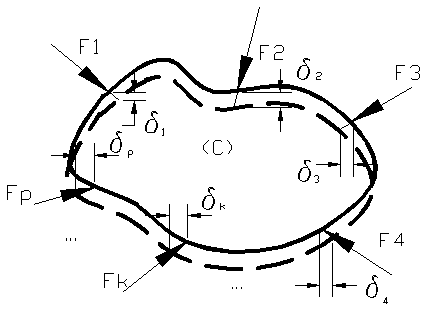
Figura 71
Acum se schimba
ordinea de aplicare a fortelor si anume : se aplica forta
elementara dFk , punctul de aplicatie al ei sufera o
deplasare infinitezimala dδk
, proiectata pe directia fortei dFk , lucrul mecanic inmagazinat in corpul (C)
este 
, pe urma se aplica fortele F1 , F2
, F3, ., Fk , Fp care va deforma corpul
, producand un lucru mecanic L . Lucrul mecanic total va fi : L + + dFk.δk (b). Forta infinitezimala dFk se afla deja pe corpul (C) si se
deplaseaza cu valoarea deplasarii produsa de forta Fk
, adica δk
, ca atare va produce un lucru mecanic dFk. δk
Produsul nu se pune cu ½ fiindca in parcurgerea sagetii δk , forta elementara dFk ramane constanta , celelalte cresc de la zero la valoarea lor finala. Se egaleaza
( a ) si ( b ) , L + = L + + dFk.δk , iar 
de unde rezulta :
δk = 
, relatia este prima teorema a lui Castigliano care se
enunta astfel: derivata partiala a expresiei energiei
potentiale de deformatie , inmagazinata intr-un corp sau sistem
elastic, in raport cu o forta concentrata , este egala cu deplasarea
din punctul de aplicatie al fortei , proiectata pe directia
si sensul ei.
S-a demonstrat in cazul fortelor concentrate , dar in mod analog se demonstreaza si pentru momentele concentrate Mk , si se ajunge la :
, ceea ce reprezinta a doua teorema a lui Castigliano care se enunta asfel
: derivata partiala a expresiei energiei potentiale de
deformatie , inmagazinata intru-un corp sau sistem elastic, in raport
cu un moment concentrat , este egala cu deplasare unghiulara din punctul de aplicatie al momentului ,
proiectatata pe directia si in sensul momentului.
2. Prima teorema lui Castigliano aplicata la solicitarea axiala Problema nr.1
Sa se calculeze deplasarea punctului C pentru bara din figura 72 , stiind ca E = 2,1 .105 MPa ; l = 0.1 m.
Pentru a afla deplasarea
punctului C , se face dlc = 
; daca avem
derivate partiale trebuie sa aflam forta de reactiune
HA functie de FC, apoi la urma se
inlocuieste FC = 10 kN.
; HA + 20 kN – 17 kN – FC
= 0 ; HA = FC – 3
kN ;
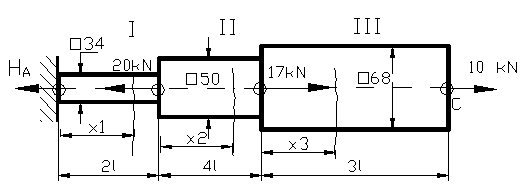Figura 72
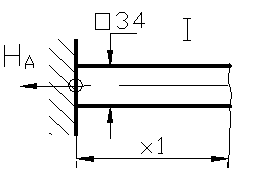
Figura 73
Regiunea intai
, N
(x1) = HA = FC
– 3 kN
Regiunea a II-a
, N
(x2) = HA + 20 kN
= FC - 3 kN +20 kN = FC
+ 17 kN Regiunea a III-a
, N
(x3) = HA + 20 kN
– 17 kN = FC - 3 kN +3kN = FC
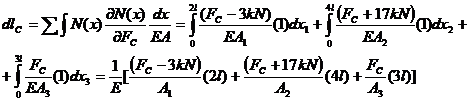
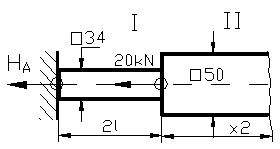
Figura 74
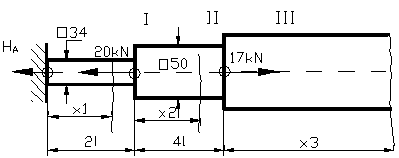
Figura 75
acum se inlocuieste FC = 10 kN si se obtine dlC = 0,029 mm.
|
Regiunea |
N(x) |
|
x |
|
intai |
Fc – 3 kN |
1 |
|
|
a II – a |
Fc + 17kN |
1 |
|
|
a III –a |
Fc |
1 |
|
