
|
|
|
Teorema de inversare locala
In cele ce urmeaza vom introduce o notiune de mare importanta si utilitate si anume notiunea de transformare regulate(difeomorfism), dupa care vom demonstra 2 rezultate fundamentale ale analizei matematice, strans legate intre ele: teorema de inversare locala si teorema functiilor implicite.
Definitia8
Fie D un deschis din Rn, Δ un deschis din Rm si F:D![]() Δ.Spunem ca F este o transformare punctuala de la D la Δ daca F este de clasa C 1 pe D.
Δ.Spunem ca F este o transformare punctuala de la D la Δ daca F este de clasa C 1 pe D.
Definitia9
Fie f:D![]() R, unde D este un deschis din Rn.
R, unde D este un deschis din Rn.![]()
a) Spunem ca
f este derivabila partial pe D daca f este derivabila partial in orice
punct a![]() D in raport cu toate variabilele xk.In
acest caz, se pot defini n functii
D in raport cu toate variabilele xk.In
acest caz, se pot defini n functii ![]() :D
:D![]() R,
R, ![]() k=
k=![]() numite derivate partiale ale lui f
pe D.
numite derivate partiale ale lui f
pe D.
b) Spunem ca f este de clasa C1 pe D
daca f este derivabila partial pe D iar functiile ![]() cu k=
cu k=![]() sunt continue pe D. Notam: f
sunt continue pe D. Notam: f![]() C1(D)
C1(D)
Exemple
1) ![]() aplicatie liniara F:Rn
aplicatie liniara F:Rn![]() Rm este transformare punctuala
Rm este transformare punctuala
2) Fie F:Rn![]() Rn , definite prinF(x)=IRn (x)+c,
Rn , definite prinF(x)=IRn (x)+c, ![]() x
x![]() Rn , c
Rn , c![]() Rn
Rn
IRn =aplicatia identical in Rn
IRn =aplicatie de clasa C1 pe Rn
F=clasa C1 pe Rn ![]() F este transformare punctuala de la Rn
la Rn .
F este transformare punctuala de la Rn
la Rn .
Definitia10
Fie D si ![]() doi deschisi din Rn si F:D
doi deschisi din Rn si F:D![]()
![]() bijectiva.Spunem ca F este o transformare regulata (difeomorfism) sau un izomorfism diferentiabil daca f este de clasa C1 pe D iar F-1
este de clasa C1 pe
bijectiva.Spunem ca F este o transformare regulata (difeomorfism) sau un izomorfism diferentiabil daca f este de clasa C1 pe D iar F-1
este de clasa C1 pe ![]()
Teorema16(de caracterizare)
Fie D si ![]() doi deschisi din Rn si F:D
doi deschisi din Rn si F:D![]()
![]() o aplicatie bijectiva a.i. F
o aplicatie bijectiva a.i. F![]() C1(D) .
C1(D) .
Atunci F este un difeomorfism ![]() pentru
pentru ![]() a
a![]() D, diferentiala dF(a):Rn
D, diferentiala dF(a):Rn![]() Rn este izomorfism liniar
si F-1 este continua.
Rn este izomorfism liniar
si F-1 este continua.
Dem.
Fie a![]() D si b=F(a)
D si b=F(a)
Sa pp ca F=difeomorfism ![]() F
F![]() C 1(D)
C 1(D)
F-1
![]() C1(
C1(![]()
![]() conform criteriului de diferentiabilitate F-1
=diferentiabila pe
conform criteriului de diferentiabilitate F-1
=diferentiabila pe ![]()
![]() F-1 =continua pe
F-1 =continua pe ![]()
Dar F![]() F-1=IRn si F-1
F-1=IRn si F-1![]() F=IRn
F=IRn
Aplicand teorema de compunere a functiilor
diferentiabile ![]() (1) JF(a)·JF-1(F(a))=En , En =matricea unitate de
ordin n.
(1) JF(a)·JF-1(F(a))=En , En =matricea unitate de
ordin n.
JF-1(F(a))·JF(a)= En
Din (1) obtinem JF(a) - matrice nesingulara si in plus
(2) JF-1(F(a))=[JF(a)]-1
Reciproc
Sa pp ca ![]() a
a![]() D, diferentiala dF(a) este un
izomorfism si, F-1 este continua.
D, diferentiala dF(a) este un
izomorfism si, F-1 este continua.
Pentru a demonstra ca F=difeomorfism, vom arata
ca finctia G=F-1 estede clasa C1 pe ![]()
G-diferentiala in orice punct b![]()
![]()
Fie b![]() D si a=G(b), adica b=F(a).
D si a=G(b), adica b=F(a).
Intrucat F-diferentiabila in a, (![]() ) T=dF(a):Rn
) T=dF(a):Rn![]() Rn si
Rn si ![]() :D
:D![]() Rn a.i. F(x)=F(a)+T(x-a)+
Rn a.i. F(x)=F(a)+T(x-a)+![]() ||x-a||,
||x-a||, ![]() x
x![]() D, unde
D, unde ![]()
Notam: J=F(x) ![]() J-b=T(x-a)+
J-b=T(x-a)+![]() ||x-a||,
||x-a||, ![]() x
x![]() D.
D.
Conform
ipotezei T-inversabil ![]() aplicand T-1 in ultima relatie obtinem:
aplicand T-1 in ultima relatie obtinem:
T-1(y-b)=x-a+T-1(![]() )||x-a||, x
)||x-a||, x![]() D
D
![]() (3) x-a=T-1(y-b)-T-1(
(3) x-a=T-1(y-b)-T-1(![]() )||x-a||,
)||x-a||, ![]() x
x![]() D
D
T-1=operator
liniar continuu ![]() (
(![]() )
) ![]() >0 a.i. ||T-1(y-b)||≤
>0 a.i. ||T-1(y-b)||≤![]() ||y-b||
||y-b||
Aplicand
norma in relatia (3) ![]()
||x-a||≤||T-1(y-b)||+||x-a||·||T-1
(![]() )||≤
)||≤![]() ||y-b||+||T-1
||y-b||+||T-1 ![]() ||·||x-a|| ,
||·||x-a|| ,![]() x
x![]() D.
D.
Daca y![]() b se vede ca:
b se vede ca:
![]()
![]()
![]() +||T-1(
+||T-1(![]()
![]()
![]() x
x![]() D
D
Sau
![]()
![]()
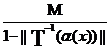
![]() x
x![]() D, adica raportul
D, adica raportul ![]() este marginit intr-o vecunatate a lui b.
este marginit intr-o vecunatate a lui b.
Din relatia (3)![]()
![]() , y
, y![]() b
b
Cum F-1=continua ![]() y
y![]() b
b ![]() x
x![]() a
a ![]()
![]() T-1(
T-1(![]() ) =0
) =0 ![]() (
(![]()
![]()
![]() , adica G-diferentiabila in b si in
plus
, adica G-diferentiabila in b si in
plus
T=operator continuu
dG(b)=T-1=[dF(a)]-1
b este arbitrar ![]() G-diferentiabila pe D. Cf.Th.(11.2.5) G este
derivabila partial pe D.
G-diferentiabila pe D. Cf.Th.(11.2.5) G este
derivabila partial pe D.
Sa aratam ca derivatela partiale ale lui G sunt continue pe D.
Observam ca in relatia (2) s-a utilizat numai diferentiabilitatea functiilor F si F-1
. Aplicam aceasta relatie perechii de functii F,G in orice punct x![]() D, avem:
D, avem:
JG(F(x)=[JF(x)]-1 .
Dar determinantul JF(x)![]() pentru orice x
pentru orice x![]() D si cum elementul lui JF(x)=functii continue(F
D si cum elementul lui JF(x)=functii continue(F![]() C1(D)
C1(D) ![]() fi
fi![]() C1(D),
C1(D), ![]() i=
i=![]() , fi componentele lui F )
, fi componentele lui F )![]()
![]() elementele matricii JG(F(x)) continue in x, ceea
ce antreneaza ca:toate derivatele partiale ale lui G in punctual y=F(x)
continue in orice x
elementele matricii JG(F(x)) continue in x, ceea
ce antreneaza ca:toate derivatele partiale ale lui G in punctual y=F(x)
continue in orice x![]() D
D ![]() F-1
F-1 ![]() C1(D).
C1(D).
Exemplu
Fie D un deschis din Rn iar
F:D![]() Rn o functie
diferentiabila pe D .Sa pp ca x0
Rn o functie
diferentiabila pe D .Sa pp ca x0 ![]() D si ca F(x0)=y0(4)
D si ca F(x0)=y0(4)
Cum x0 este punct
interior lui D ![]() (
(![]() )S(x0,r)
)S(x0,r)![]() D.
D.
Se pun urmatoarele intrebari?
1)Poate fi oare rezolvata
ecuatia F(x)=y in raport cu x![]() S(x0,r)pentru orice y
S(x0,r)pentru orice y![]() Rn sau macar pentru y
dintr-o multime precizata?
Rn sau macar pentru y
dintr-o multime precizata?
2)Daca (![]() ) o asemenea solutie y=
) o asemenea solutie y=![]() a ecuatiei f(x)=y este oare ea
unica?
a ecuatiei f(x)=y este oare ea
unica?
3)Daca (![]() ) functia
) functia ![]() , in ce conditii aceasta solutie este
diferentiabila?
, in ce conditii aceasta solutie este
diferentiabila?
Ex
Fie functia f:R![]() R, definite prin f(x)=x2
R, definite prin f(x)=x2 ![]() f(0)=0
f(0)=0 ![]() in relatia (4) x0=0=y0
in relatia (4) x0=0=y0
Daca y<0 ![]() ecuatia f(x)=y nu are nici o solutie
ecuatia f(x)=y nu are nici o solutie
Daca y>0 ![]() observam ca pentru x dintr-o
vecinatate a lui 0 ecuatia y=x2 are 2 solutii, deci ecuatia f(x)=y
admite solutii, dar aceasta nu este unica.
observam ca pentru x dintr-o
vecinatate a lui 0 ecuatia y=x2 are 2 solutii, deci ecuatia f(x)=y
admite solutii, dar aceasta nu este unica.
Observam ca daca y>0 si x0>0
putem indica o vecinatate (x0-![]() , x0+
, x0+![]() ) a punctului x0 a.i.
ecuatia f(x)=y , adica y=x2 sa aiba o singura solutie x=
) a punctului x0 a.i.
ecuatia f(x)=y , adica y=x2 sa aiba o singura solutie x=![]() in vecinatatea (x0-
in vecinatatea (x0-![]() , x0+
, x0+![]() ).In plus, aceasta solutie este si
derivabila pe multimea (x0-
).In plus, aceasta solutie este si
derivabila pe multimea (x0-![]() , x0+
, x0+![]() ).Aceste exemple arata ca, daca nu
intotdeauna putem rezolva problema propusa pe intreaga multime de definitie a
functiei, totusi, ea poate fi rezolvata macar local, in anumite situatii.
).Aceste exemple arata ca, daca nu
intotdeauna putem rezolva problema propusa pe intreaga multime de definitie a
functiei, totusi, ea poate fi rezolvata macar local, in anumite situatii.
Lema1
Fie x0![]() Rn, T(x0,r)-sfera
inchisa de centru x0 si de raza r din Rn si F: T(x0,r)
Rn, T(x0,r)-sfera
inchisa de centru x0 si de raza r din Rn si F: T(x0,r)![]() Rn .Daca functia
Rn .Daca functia ![]() =F(x)-x,
=F(x)-x, ![]() x
x![]() T(x0,r) este o contractie
de constanta k, atunci (
T(x0,r) este o contractie
de constanta k, atunci (![]() ) o vecinatate deschisa V a punctului
x0 a.i. V
) o vecinatate deschisa V a punctului
x0 a.i. V![]() T(x0,r) iar restrictia
lui F la V sa defineasca un homeomorfism intre functia F|V este
lipschitzina de constanta1/(1-k)
T(x0,r) iar restrictia
lui F la V sa defineasca un homeomorfism intre functia F|V este
lipschitzina de constanta1/(1-k)
Dem.
fie y![]() S(y0,(1-k)r).Se observa ca
functia H(x)=y-
S(y0,(1-k)r).Se observa ca
functia H(x)=y-![]()
![]() x
x![]() T(x0,r) este tot o
contractie de constanta k si transforma multimea T(x0,r) in ea
insasi.
T(x0,r) este tot o
contractie de constanta k si transforma multimea T(x0,r) in ea
insasi.
||H(x)-H(x')||=||y-![]() -y+
-y+![]() (x')||=||
(x')||=||![]()
![]() (x')||≤k||x-x'||,
(x')||≤k||x-x'||, ![]() x,x'
x,x'![]() T(x0,r), ceea ce spune ca
H=contractie iar daca x
T(x0,r), ceea ce spune ca
H=contractie iar daca x![]() T(x0,r), adica ||x-x0||≤r,
avem:
T(x0,r), adica ||x-x0||≤r,
avem:
||H(x)-x0||=||y-![]() (x)-x0||=||y-F(x0)+F(x0)-
(x)-x0||=||y-F(x0)+F(x0)-![]() (x)-x0||≤||y-y0||+||
(x)-x0||≤||y-y0||+||![]() (x0)-
(x0)-![]() (x)||≤(1-k)r+kr=r, ceea ce
spune ca H(x)
(x)||≤(1-k)r+kr=r, ceea ce
spune ca H(x)![]() T(x0,r),
T(x0,r), ![]() x
x![]() T(x0,r)
T(x0,r)
Cum T(x0,r) este
multime inchisa in spatiul metric complet Rn ![]() T(x0,r) subspatiu complet.
T(x0,r) subspatiu complet.
Atunci functia H satisface
ipoteza principala de punct fix al lui Banach.Deci pentru fiecare y![]() S(y0,(1-k)r) (
S(y0,(1-k)r) (![]() )un punct unic xy
)un punct unic xy![]() T(x0,r) a.i. y=
T(x0,r) a.i. y=![]() (x)=xy sau y=F(xy).
(x)=xy sau y=F(xy).
Fie V=F-1(S(yo,(1-k)r)).Atunci F|V bijectiva intre V si S(y0,(1-k)r)
![]() =contractie, es este functie continua
=contractie, es este functie continua
![]() F=
F=![]() -IRn=continua.
-IRn=continua.
Cum S(y0,(1-k)r)
-deschisa si F -continua ![]() V-deschisa
V-deschisa
Fie G inverse restrictiei lui F la V.
G -lipschitziana de constanta 1/(1-k) pe S(y0,(1-k)r)
In adevar
||G(y1)-G(y2)||=||x1-x2||≤||x1-F(x1)-x2+F(x2)||+||F(x1)-F(x2)||=||![]() (x2)-
(x2)-![]() (x1)||+||y1-y2||≤k||x1-x2||+||y1-y2||=k||G(y1)-G(y2)||+||y1-y2||,
(x1)||+||y1-y2||≤k||x1-x2||+||y1-y2||=k||G(y1)-G(y2)||+||y1-y2||,
![]() y1,y2
y1,y2![]() S(y0,(1-k)r), adica G este lipschitziana
deconstanta 1/(1-k).
S(y0,(1-k)r), adica G este lipschitziana
deconstanta 1/(1-k).
Prin urmare G=continua si atunci functia F|V:V![]() S(y0,(1-k)r) - homeomorfism.
S(y0,(1-k)r) - homeomorfism.
Teorema17 (th de inversare locala)
Fie D un deschis din Rn, F:D![]() Rn functie de clasa C1
pe D si a
Rn functie de clasa C1
pe D si a![]() D.Daca dF(a):Rn
D.Daca dF(a):Rn![]() Rn -operator liniar
invresabil, atunci (
Rn -operator liniar
invresabil, atunci (![]() ) o vecinatate deschisa V
) o vecinatate deschisa V![]() D a lui a a.i. F(V)=deschis din Rn
iar F sa stabileasca un difeomorfism intre v si F(V)
D a lui a a.i. F(V)=deschis din Rn
iar F sa stabileasca un difeomorfism intre v si F(V)
Dem.
Fara a micsora generalitatea rezultatului pp
a=0 si b=F(a)=0.(in caz contrar, consideram translatiile de vector a si b=F(a)
-difeomorfism, ![]() =x-a,
=x-a,
![]() =y-b si functia G(
=y-b si functia G(![]() )=F(
)=F(![]() +a)-F(a) atunci G satisface cond th
si in plus G(0)=F(a)-F(a)=0)
+a)-F(a) atunci G satisface cond th
si in plus G(0)=F(a)-F(a)=0)
Pp si ca dF(0)= IRn , intrucat daca T=dF(0)+ IRn , putem considera functia
(5) H=T-1
![]() F pentru care H(0)=T-1(F(0))=T-1(0)=0
si care este diferntiabila in virtutea th de compunere a functiilor
diferentiabile.
F pentru care H(0)=T-1(F(0))=T-1(0)=0
si care este diferntiabila in virtutea th de compunere a functiilor
diferentiabile.
Cf. th.11.2.7. si 11.1.7 ![]() relatia dH(0)=dT-1(F(0))
relatia dH(0)=dT-1(F(0))![]() dF(0)=dT-1(0)
dF(0)=dT-1(0)![]() T=T-1
T=T-1 ![]() T= IRn
T= IRn
Daca pp ca th are loc pt H
atunci va (![]() )o vecinatate deschisa a originii, V
)o vecinatate deschisa a originii, V![]() D, a.i. restrictia lui H la V
-bijectie intre V si H(V) iar H-1
D, a.i. restrictia lui H la V
-bijectie intre V si H(V) iar H-1 ![]() C1(H(V)), adica H|V
- difeomorfism
C1(H(V)), adica H|V
- difeomorfism ![]() (5) T
(5) T![]() H=T
H=T![]() T-1
T-1![]() F=F, adica restrictia lui F la V este
difeomorfism intre V si F(V)
F=F, adica restrictia lui F la V este
difeomorfism intre V si F(V) ![]() th. Este adevarata si pt F.
th. Este adevarata si pt F.
Pp a=0, b=F(0) si dF(0)= IRn
Fie functia ![]() :D
:D![]() Rn definite prin:
Rn definite prin:
(6) ![]() (x)=F(x)-x,
(x)=F(x)-x, ![]() x
x![]() D
D
Cum F![]() C1(D)
C1(D) ![]()
![]() C1(D)
C1(D)
In plus ![]() (0)=0,d
(0)=0,d![]() (0)=dF(0)- IRn= IRn- IRn=0
(0)=dF(0)- IRn= IRn- IRn=0
Vom arata, in continuare , ca (![]() )r>0 a.i. functia
)r>0 a.i. functia ![]() - contractie pe o
sfera inchisa T(0,r)
- contractie pe o
sfera inchisa T(0,r)![]() D.
D.
Deoarece ![]()
![]() C1(D), iar derivatele partiale ale functiilor
componente ale lui
C1(D), iar derivatele partiale ale functiilor
componente ale lui ![]() =(
=(![]() ) sunt nule I origine, (
) sunt nule I origine, (![]() ) o vecinatate U a originii a.i. functiil (
) o vecinatate U a originii a.i. functiil (![]() ), k=
), k=![]() sa verifica inegalitatea||d
sa verifica inegalitatea||d![]() (t)||<
(t)||<![]() ,
, ![]() t
t![]() U, k=
U, k=![]()
Aplicam th de medie ![]()
||![]() (x')-
(x')-![]() (x'')||<
(x'')||< ![]() ||x'-x''||,
||x'-x''||, ![]() x',x''
x',x''![]() U
U
![]() (7) ||
(7) ||![]() (x')-
(x')-![]() (x'')||=
(x'')||=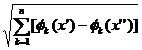 2 ≤
2 ≤![]() ||x'-x''||,
||x'-x''||, ![]() x',x''
x',x''![]() U
U
Vom allege un r>0 a.i.
T(0,r)![]() U
U
Din (7) se observa ca ![]() -contractie pentru U
-contractie pentru U ![]() este contractie si pe T(0,r) de constanta
k=1/2
este contractie si pe T(0,r) de constanta
k=1/2
Deoarece ![]() - contractie, functia F:T(0,r)
- contractie, functia F:T(0,r)![]() Rn satisface conditiile
lemei
Rn satisface conditiile
lemei ![]()
![]() ) o vecinatate deschisa U1
a punctului 0 a.i. U1
) o vecinatate deschisa U1
a punctului 0 a.i. U1![]() T(0,r) iar restrictia lui F la U1
este un homeomorfism intre U1 si sfera deschisa S(0,(1-1/2)r)=S(0,r/2).
T(0,r) iar restrictia lui F la U1
este un homeomorfism intre U1 si sfera deschisa S(0,(1-1/2)r)=S(0,r/2).
Observam ca F|U1 - bijectie intre U1 si F(U1), este de clasa C1 pe U1 iar inversa functiei F|U1 - continua pe S(0,r/2), fiind homeomorfism.
Intrucat matricea jacobiana JF - nesingulara in origine, operatorul T=dF(0) -fiind inversabil, iar elementele sale fiind functii continue.
F![]() C1(D)
C1(D) ![]() JF -
matrice nesingulara pe o vecinatate deschisa V a originii cu V
JF -
matrice nesingulara pe o vecinatate deschisa V a originii cu V![]() U1
U1 ![]()
F|V - bijectie intre V si F(V), F(V) -deschis din Rn (F - homeomorfism)
F![]() C1(V), F-1 - continua iar matricea JF(x)
- nesingulara pentru
C1(V), F-1 - continua iar matricea JF(x)
- nesingulara pentru ![]() x
x![]() V.
V.
Cf. th.11.4.3 ![]() F|V - difeomorfism intre V si F(V).
F|V - difeomorfism intre V si F(V).
Corolar7
Fie F:D![]() Rn o aplicatie de clasa C1 pe deschisul
D din Rn a.i. matricea jacobiana JF(x) - nesingulara in
orice x
Rn o aplicatie de clasa C1 pe deschisul
D din Rn a.i. matricea jacobiana JF(x) - nesingulara in
orice x![]() D.Atunci F=este o aplicatie deschisa, adica transforma
deschisi in deschisi.
D.Atunci F=este o aplicatie deschisa, adica transforma
deschisi in deschisi.
Dem.
Fie A un deschis din D si fie
y0 ![]() F(A).Atunci (
F(A).Atunci (![]() ) x0
) x0 ![]() A a.i. F(x0)=y0
A a.i. F(x0)=y0
Cf. th. De inversare locala
aplicata pe multimea A, (![]() ) V
) V![]() V (x0) a.i. V
V (x0) a.i. V![]() A si F(V) sa fie deschisa.
A si F(V) sa fie deschisa.
Din th. 11.2.11 conditia ca matricea JF(x)
sa fie nesingulara in ![]() x
x![]() D
D ![]() dF(x) - izomorfism liniar.
dF(x) - izomorfism liniar.
Dar y0 ![]() F(V)
F(V)![]() F(A)
F(A) ![]() F(A) - vecinatate pentru y0
si cum y0 -arbitrar in F(A)
F(A) - vecinatate pentru y0
si cum y0 -arbitrar in F(A) ![]() F(A) - multime deschisa.
F(A) - multime deschisa.
Corolar8
Fie fi:D![]() R, i=
R, i=![]() , n functii de clasa C1 pe
deschisul D din Rn .Daca (
, n functii de clasa C1 pe
deschisul D din Rn .Daca (![]() )un punct a
)un punct a ![]() D a.i.
D a.i. ![]() pentru
pentru ![]() y=(y1,y2,.,yn)
y=(y1,y2,.,yn)![]() U
U
Sistemul de ecuatii 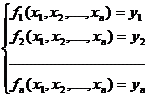 are solutie unica intr-o vecinatate a
punctului a
are solutie unica intr-o vecinatate a
punctului a
Dem.
Fie functia vectoriala F:D![]() Rn ale carei componente
sunt functiile date f1,f2,.,fn.
Rn ale carei componente
sunt functiile date f1,f2,.,fn.
Observam ca F satisface conditiile
din th de inversare locala si atunci (![]() ) o vecinatate deschisa V a punctului
a a.i. V
) o vecinatate deschisa V a punctului
a a.i. V![]() D si F - difeomorfism intre V si
F(V)=U.
D si F - difeomorfism intre V si
F(V)=U.
Multimea U satisface
conditiile cerute de probleme intrucat pentru orice y=(y1,y2,.,yn)![]() U ecuatia F(x)=y are solutia unica x
U ecuatia F(x)=y are solutia unica x![]() V.
V.
Functii implicite
Fie f:E![]() R o functie definite pe E
R o functie definite pe E![]() R2 si fie ecuatia
R2 si fie ecuatia
(8) f(x,y)=0
pp. ca f(x0,y0)=0, unde (x0,y0)- punct din E.
se pune problema relatia (8)
poate fi rezolvata in raport cu y, adica daca (![]() ) o functie
) o functie ![]() definite pe o multime V
definite pe o multime V![]() V(x0), x0
V(x0), x0![]() R a.i. y=
R a.i. y=![]() (x) si f(x,
(x) si f(x,![]() (x))=0,
(x))=0, ![]() x
x![]() V.
V.
mai mult am dori ca aceasta solutie sa fie unica si sa fie o functie diferentiabila.
O asemenea solutie y=![]() (x) se numeste functie implicita
pentru ca relatia(8) il determinam pe y in functie de x fara insa a aparea o
formula explicita.
(x) se numeste functie implicita
pentru ca relatia(8) il determinam pe y in functie de x fara insa a aparea o
formula explicita.
Ex.
Fie functia f(x,y)=x2+y2-1
Daca consideram punctual (1,0)
![]() f(x,y)=0
f(x,y)=0 ![]() x2+y2-1=0
x2+y2-1=0 ![]() y2=1-x2
y2=1-x2 ![]() y=
y=![]()
![]()
Observam ca problema nu are solutie unica in jurul punctului (1,0).
y=![]() (x)
(x) ![]() y=
y=![]()
![]() y'=
y'=![]()
![]() nu este derivabila in
x0=1
nu este derivabila in
x0=1
![]()
Daca consideram punctual (![]() )
) ![]() f(
f(![]() )=1/2+1/2-1=0
)=1/2+1/2-1=0
Iar ![]()
![]()
![]() )=2·
)=2·![]()
![]()
![]()
![]()
![]() pot indica o vecinatate a punctului x0=
pot indica o vecinatate a punctului x0=![]() a.i. solutia y=
a.i. solutia y=![]() sa fie unic determinat.
sa fie unic determinat.
Mai mult, pe o asemenea
vgecinatate y=![]() (x)=
(x)=![]() - derivabila
- derivabila
Teorema18 (th. Functiilor implicite)
Fie D un deschis din Rn![]() Rm, f:D
Rm, f:D![]() Rm o functie vectoriala de
componente (f1,f2,..,fm) si (x0,y0)
Rm o functie vectoriala de
componente (f1,f2,..,fm) si (x0,y0)![]() D.
D.
Daca sunt indeplinite conditiile:
1.f(x0,y0)=0
2.f![]() C1(D)
C1(D)
3.![]()
![]()
Atunci (![]() ) o vecinatate deschisa I a punctului
x0 in Rn, o vecinatate deschisa J a punctului y0
in Rm si a functiei
) o vecinatate deschisa I a punctului
x0 in Rn, o vecinatate deschisa J a punctului y0
in Rm si a functiei ![]() :I
:I![]() j a.i.
j a.i.
I.
f(x,![]() (x))=0,
(x))=0, ![]() x
x![]() I
I
II.
f(x,y)=0 pentru (x,y)![]() I
I![]() J
J ![]() y=
y=![]() (x)
(x)
III.
![]() - diferentiabila pe I
- diferentiabila pe I
Dem.
Definim
urmatoarea functie F:D![]() Rn
Rn![]() Rm prin egalitatea:
Rm prin egalitatea:
(9) F(x,y)=(x,f(x,y)), ![]() (x,y)
(x,y)![]() D.
D.
Atunci
JF(x0,y0)=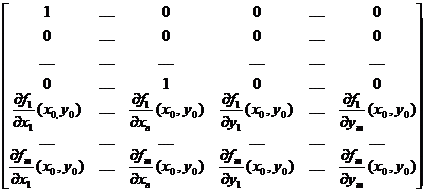
![]() det JF(x0,y0)=
det JF(x0,y0)=![]()
![]() 0
0
Se observa ca F satisface conditia th. De
inversare locala (F![]() C1(D), JF(x0,y0)
-nesingulara )
C1(D), JF(x0,y0)
-nesingulara ) ![]() (
(![]() ) o vecinatate deschisa U
) o vecinatate deschisa U![]() V(x0,y0) a.i. U
V(x0,y0) a.i. U![]() D
D
(![]() ) o vecinatate deschisa W1
=F(U) a punctului F(x0,y0)=(x0,f(x0,y0))=(x0,0)
a.i. F difeomorfism intre U si W1 .
) o vecinatate deschisa W1
=F(U) a punctului F(x0,y0)=(x0,f(x0,y0))=(x0,0)
a.i. F difeomorfism intre U si W1 .
Fara a micsora generalitatea, putem pp ca U este
de forma I0 ![]() J,
J,
unde I0 - deschis din Rn ce contine x0J - deschis din Rn ce contine y0
Daca notam cu I= observam ca
I - vecinatate deschisa a punctului x0
, I![]() I0 iar F(I
I0 iar F(I![]() J)=W - vecinatate deschis a punctului
(x0,0)
J)=W - vecinatate deschis a punctului
(x0,0)
Fie G - inversa restrictiei lui F la I![]() J, din cele de mai sus
J, din cele de mai sus ![]() G - diferentiabila pe W.
G - diferentiabila pe W.
G=(g1,g2),
unde g1:W![]() Rn in care g1(x,y)=x,
Rn in care g1(x,y)=x, ![]() (x,y)
(x,y)![]() W iarg2:W
W iarg2:W![]() Rm g2
- functie diferentiabila pe W.
Rm g2
- functie diferentiabila pe W.
Fie ![]() :Rn
:Rn![]() Rm
Rm ![]() Rm functie definite prin:
Rm functie definite prin: ![]() (x,y)=y,
(x,y)=y, ![]() x
x![]() Rn
Rn
y![]() Rn
Rn
Se observa ca ![]() F=f
F=f![]() f(x,g2(x,y))=(f
f(x,g2(x,y))=(f![]() G)(x,y)=(
G)(x,y)=(![]()
![]() F
F![]() G)(x,y)=
G)(x,y)=![]() (x,y)=y
(x,y)=y
In particular f(x,g2(x,0))=0(10)
Daca
se considera functia ![]() :I
:I![]() J definita prin
J definita prin ![]() (x)=g2(x,0),
(x)=g2(x,0), ![]() x
x![]() I atunci aceasta corespunde problemei
I atunci aceasta corespunde problemei
Din
(10) ![]() f(x,
f(x,![]() (x))=0,
(x))=0, ![]() x
x![]() I (I)
I (I)
Daca f(x,y)=0 cu (x,y)![]() I
I![]() J
J ![]() F(x,y)=(x,f(x,y))=(x,0),
F(x,y)=(x,f(x,y))=(x,0), ![]() (x,y)
(x,y)![]() I
I![]() J
J
Aplicand G avem:
(G![]() F)(x,y)=G(x,0)=(x,g2(x,0))=(x,
F)(x,y)=G(x,0)=(x,g2(x,0))=(x,![]() (x)), adica (x,y)=(x,
(x)), adica (x,y)=(x,![]() (x))
(x)) ![]() y=
y=![]() (II)
(II)
Observam
ca , in particular y0=![]() (x0)
(x0)
In
sfarsit, cum g2 - diferentiabila ![]()
![]() (x)=g2(x,0),
(x)=g2(x,0), ![]() x
x![]() I -diferentiabila (III)
I -diferentiabila (III)
Cazuri particulare
1)Daca D - deschis din R2 , f:D![]() R, (x0,y0)
R, (x0,y0)![]() D si sunt indeplinite conditiile:
D si sunt indeplinite conditiile:
1)f(x0,y0)=0
2)f![]() C1(D)
C1(D)
3)![]() ( x0,y0)
( x0,y0)![]() 0
0
Atunci (![]() ) o vecinatate deschisa I a punctului x0
) o vecinatate deschisa I a punctului x0![]() R, o vecinatate deschisa J a
punctului y0
R, o vecinatate deschisa J a
punctului y0 ![]() R si o functie
R si o functie ![]() :I
:I![]() J a.i.
J a.i.
I)f(x,![]() (x))=0,
(x))=0, ![]() x
x![]() I
I
II)f(x,y)=0
, (x,y)![]() I
I![]() J
J
III) ![]() - derivabila pe I
- derivabila pe I
IV) ![]() (x0)=y0
(x0)=y0
Pentru a
calcula derivate lui ![]() vom deriva identitatea in raport cu x
vom deriva identitatea in raport cu x
(11)f((x,![]() (x))=0,
(x))=0, ![]()
![]() I
I
Utilizam regula de derivare a functiilor compuse
![]() (12)
(12) ![]() ·
·![]() =0
=0
![]()
![]() '(x)=
'(x)=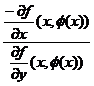 , x
, x![]() I1
I1 ![]() I in care I1
=
I in care I1
=
2) Daca D este un deschis din
R2![]() R iar f:D
R iar f:D![]() R satisface conditia din th.
Precedenta atunci relatia f(x,y,z)=0, vom putea gasi local pe z functie de x si y.
R satisface conditia din th.
Precedenta atunci relatia f(x,y,z)=0, vom putea gasi local pe z functie de x si y.
F(x,y,z(x,y))=0
Derivam in raport cu x si y ![]() derivatele partiale ale functiei z in raport
cu x si y.
derivatele partiale ale functiei z in raport
cu x si y.
(13) ![]()
![]() =0
=0 ![]()
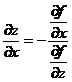
Si
(14)![]()
![]() =0
=0 ![]()
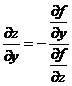
Ex.
Sa se arate ca sistemul de ecuatii
(*)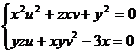
determina in mod unic u si v ca functii de
x,y,z intr-o vecinatate a punctului (u,v,x,y,z)=(0,1,3,3,-3) si s a se gaseasca
![]()
Fie functia vectoriala
F(u,v,x,y,z)=(f1(u,v,x,y,z),f2(u,v,x,y,z)), de unde ![]() f1(u,v,x,y,z)=x2u2+xzv+y2,
iar f2(u,v,x,y,z)=yzu+xyv2-3x;
f1(u,v,x,y,z)=x2u2+xzv+y2,
iar f2(u,v,x,y,z)=yzu+xyv2-3x;
F:R2![]() R3
R3![]() R2 si F
R2 si F![]() C1(R2
C1(R2![]() R3), intrucat evident
functiile f1,f2 sunt de clasa C1 pe R2
R3), intrucat evident
functiile f1,f2 sunt de clasa C1 pe R2![]() R3. Se vede ca
F(0,1,3,3,-3)=(0,0). Sa calculam
R3. Se vede ca
F(0,1,3,3,-3)=(0,0). Sa calculam
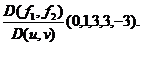
Cum ![]() ,
, ![]() ,
, ![]() ,
, ![]() obtinem
obtinem
![]() =-81
=-81![]() 0
0
Conform teoremei functiilor implicite, u si v pot fi determinati in mod unic in raport cu x,y,z intr-o vecinatate a punctului (0,1,3,3,-3).
Pentru a obtine derivatele lor partiale vom tine seama de teorema lantului(teorema de diferentiere compusa).
Atunci, dericand in raport cu x cele doua ecuatii ale sistemului (*) si, tinand seama ca u si v sunt functii de x, obtinem:
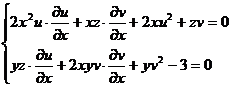
Utilizand regula lui Cramer, avem
![]()
![]()
In acelasi mod, derivand
succesiv cele doua relatii din (**) in raport cu y si cu z, se obtin derivatele
partiale ![]()
![]() si respective
si respective ![]()
![]()