|
|
|
I. Erori in cadrul sondajului statistic.
II. Tipuri de sondaje utilizate in analiza fenomenelor economice
I. In cadrul sondajului statistic se intalnesc 2 principale tipuri de erori:
de inregistrare, comune tuturor tipurilor de cercetari statistice
de reprezentativitate, proprii sondajului statistic. Acestea sunt interpretate ca erori sistematice, determinate de nerespectarea stricta a caracterului aleator de introducere a unitatilor in esantion (acestea pot fi evitate si erori de reprezentativitate intamplatoare (nu pot fi evitate deoarece esantionul nu poate reproduce identic populatia de origine).
In
teoria sondajului se demonstreaza ca: daca se realizeaza un
nr Kj suficient de mare de sondaje, media mediilor acestor sondaje Xi, i =
1,K , iar madea mediilor este o
estimatie cat mai corecta (cand K tinde spre , X este o estimatie absolut corecta a mediei
pe total) cu dispersia:
k2
2 a(Xi - X) fi
m=i=1
k
afi
i=1
si cu abaterea medie patratica ce va reprezenta eroarea medie sau eroarea de reprezentativitate.
Deoarece in practica nu se
poate realiza un K numar suficient de mare de esantionari, m se determina conform teoriei sondajului din relatia ce
exista intre volumul esantionului n, dispersia mediilor de sondaj de
la media lor si dispersia totala t cunoscuta sau
apreciata in functie de o cercetare anterioara).
Eroarea limita se not ∆x, interpretata ca o limita pana la care se accepta in anumite conditii de probabilitate, diferenta dintre media de sondaj si media totala
∆x = tmx (coeficient de probabilitate t).
Scopul oricarui sondaj
statistic este caracterizarea populatiei totale. De regula,
aceasta caracterizare se realizeaza fie in functie de nivelul
mediu alunei variabile( X ) fie pe baza marimii totalizate a acelei
variabile.
(Xs - ∆x) < Xt <(Xs + ∆x)
lim inf lim sup
N(Xs - ∆x) <
∑x < (X + ∆x)N
II. Sondajul simplu: aleator repetat si nerepetat. Se utilizeaza in situatia in care, conform scopului cercetarii, Pt (populatia totala) poate fi privita doar ca un summum de unitati.
Ex: pentru determinarea nivelului mediu si marimii totale a cheltuielilor facute de persoanele dintr-o anumita zona pentru procurarea produsului A se realizeaza un sondaj asupra unui numar de persoane ce reprezinta 0,5% din totalul zonei.
Se obtine urmatoarea situatie :
Grupe de pers.Nr. pers
dupa mil lei
5 -7 25
7 -9 70
9 -11 175
11 -13 300
13 -15 500
15 -17 200
17 -19
100
Total 1370.
n = 1370
N = 274000
Sa se aprecieze limitele intre care se vor incadra nivelul mediu al chelt si marimea totala a acestora la niv zonei. Rezultatele vor fi garantate cu o probabilitate de p = 0,95% pt care coef de probabilitate t = 0,96
∑n 6 * 25 + 8 * 70 + 10 * 175 +. + 18 * 100
Xs = == 13,182482
n 1370
∆x = pt sondajul simplu aleator repetat = tμx = + 1,39
2
μx =
n
2
2[ ( x - X ) ] n (6
- 13.18) 25 + ( 8 - 13.18)70 + + ( 18 - 13.18) 100
==
∑ n 1370
= 7,01
7.01
mx = = + 0,71
1370
Sondajul simplu aleator nerepetat
Xs= 13.8
Sondajul aleator tipic se utilizeaza in analiza marilor populatii statistice in care actiunea unor factori esentiali de regula determina organizarea unitatilor in anumite clase, grupe tipice de unitati. Scopul cercetarii este acelasi ca la sondajul simplu.
Ca tip de problematica se mentine scopul sau functia obiectiv de la sondajul simplu. In urma efectuarii sondajului s-a obtinut urmatoarea grupare a persoanelor estimate dupa nivelul ven si dupa chelt facute pt produsul A.
Gruparea dupa ven Gruparea dupa chelt Nr persoane
(mil lei)
(mil lei)
V < 60 5 - 7 25
7 - 9 70
9 - 11 25
TOTAL 120
V > 60; 9 - 11 150
V < 200 11
- 13 300
13
- 15 500
15
- 17 100
TOTAL 1050
V > 200 15
- 17 100
17 - 19 100
TOTAL 200
TOTAL 1370
Sondajul tipic aleator repetat.
Xs - ∆x< ∆t < Xs + ∆
N(Xs - ∆x) < ∑ x < (Xs + ∆x)N
X1 = 82
X2 = 13.04 2
1 = 2 2=3,14
X3 =17 2
3 = 1
8 * 120 + 13.04 * 1050 + 17 * 200
Xs = medie
de sondaj = ≈ 15
1370
2
2 ∑ ni
=
∑ ni
2 2
* 120 + 3.14 * 1050 + 1200
Media dispersiilor: = ≈ 3.12
1370
Sondajul tipic aleator nerepetat :
2
μx = N - n
n N -
1
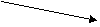
0.9974
Sondajul de serii : in situatiile in care anuitatile singale ale populatiei totale sunt organizate in R serii sau grappe. In esantion se vor extrage un numar reprezentativ de r serii formate din acelasi numar de unitati simple si in aceeasi compunere ca in cea existenta in populatia totala. La nivelul fiecarei i serii, i = 1,r se determina media: Xi pentru variabila analizata. La nivelul esantionului se inregistreaza o dispersie a acestor medii fata de media lor ( care va evidentia media de sondaj).
r ( Xi
- X)
dx = ∑ dispersia medie dintre serii
r
Pentru sondajul de serii aleator repetat:
Xs - ∆x < Xt < Xs + ∆x
Xs = X
∆x = t
μx
δx
μx =
r
Pentru sondajul de serii aleator nerepetat :
δ R - r
μx=
r R - 1
