
|
|
|
Schema motorului de curent continuu cu excitatie independenta este data in figura 1.
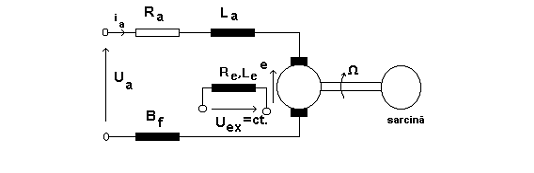
Figura 3.1 - schema MCC - IND.
Presupunand excitatia independenta a motorului cu curent de excitatie constant, ecuatiile care descriu functionarea motorului se obtin aplicand teorema a doua al lui Kirchhoff circuitului rotoric al motorului si legea echilibrurilor cuplurilor, care intervin in functionarea acestuia.
Ecuatiile motorului sunt:
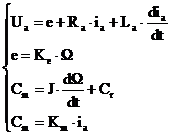
Unde: ![]() - tensiunea de
alimentare a circuitului rotoric;
- tensiunea de
alimentare a circuitului rotoric;
E - tensiunea electromotoare a motorului;
![]() - rezistenta
circuitului indusului (rotor);
- rezistenta
circuitului indusului (rotor);
![]() - inductivitatea
circuitului indusului;
- inductivitatea
circuitului indusului;
![]() - curentul rotoric
absorbit de motor;
- curentul rotoric
absorbit de motor;
![]() - viteza
unghiulara a axului motorului;
- viteza
unghiulara a axului motorului;
Ke, Km - constante de proportionalitate;
J - moment de inertie;
![]() - cuplu motor;
- cuplu motor;
![]() - cuplu rezistent;
- cuplu rezistent;
Curentul
nominal rotoric se determina cu relatia ![]() ;
;
![]()
Curentul limita (la pornire):
![]()
Rezistenta circuitului rotoric:
![]()
Rezistenta bobinei de filtraj:
![]()
unde ![]() caderea de
tensiune pe bobina de filtraj Bf (se ia 2.5%*Un)
caderea de
tensiune pe bobina de filtraj Bf (se ia 2.5%*Un)
Rezistenta totala a circuitului rotoric:
![]() .
.
Inductivitatea circuitului rotoric:
![]()
Inductivitatea bobinei de filtraj:
![]() ;
;
Inductivitatea totala:
![]() ;
;
![]() ;
;
Determinarea constantelor de proportionalitate din ecuatia motorului:
![]() ;
;
![]() ;
;
![]() ;
;
Moment de inertie:
![]() ;
;
Se determina parametrii care intervin in modelul ISO al motorului:
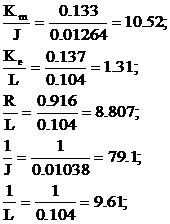
Cu aceste elemente ecuatia motorului se transforma in limbaj intrare-stare-iesire respectiv se obtine modelul ISO.
Introducerea variabilelor de stare:
![]() - pozitia
unghiulara a axului motorului;
- pozitia
unghiulara a axului motorului;
![]() - viteza
unghiulara;
- viteza
unghiulara;
![]() - curentul indusului;
- curentul indusului;
Definim notatiile
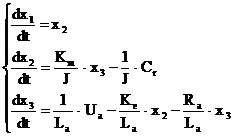
Ecuatiile de mai sus scrise in forma matriciala arata astfel:
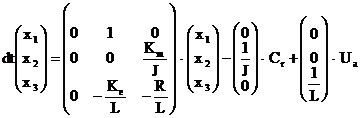
![]()
Se vor determina valorile numerice ale acestor ecuatii matriceale. Se considera cuplul rezistent Cr = 0. Se considera conditiile initiale nule:
x1(0)=0 x2(0)=0 x3(0)=0
Astfel se obtin matricile sistem:
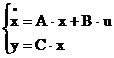
unde s-a notat:
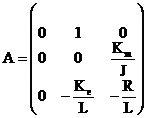
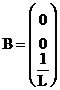 ;
;
![]() .
.
Cu parametrii determinati mai sus se calculeaza valorile numerice ale matricelor A, B si C.
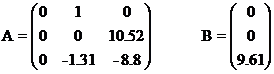
![]()
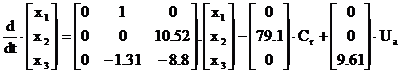
Folosind acest model se va determina raspunsul sistemului la o intrare treapta unitara ua(t)=1 si cuplu rezistent 0. Se vor determina grafic traiectoriile de stare x1(t), x2(t), x3(t) si y(t). Pe baza acestor raspunsuri se va studia stabilitatea sistemului. Pentru a trasa traiectoriile de stare se va folosi programul SIMULINK sub MATLAB. Modelul ISO al sistemului se aduce la forma:
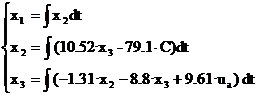
Acest model se va construi
usor in mediul SIMULINK.
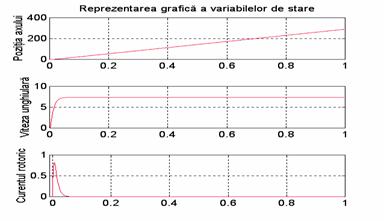
Simularea
se va realiza folosind metoda numerica
Runge-Kutta. Modelarea s-a facut intr-un interval de timp de 20 [s]. Valorile
variabilelor de stare obtinute se vor reprezenta in functie de timp
prezentat in figura urmatoare:
![]()
Aplicand transformata
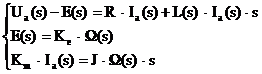
Inlocuind ultimile doua ecuatii in prima ecuatie vom obtine:
![]()
Din relatia de mai sus rezulta functia de transfer:
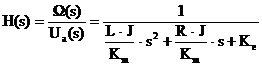
Facand inlocuirile:
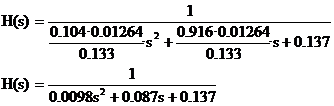
Daca marimea de iesire se considera pozitia axului rotoric vom avea:
![]()
cu care functia de transfer devine:
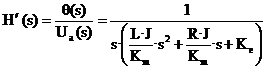
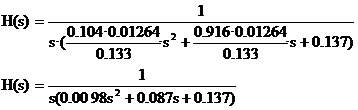
Schema echivalenta rezultata din modelarea acestor ecuatii este:
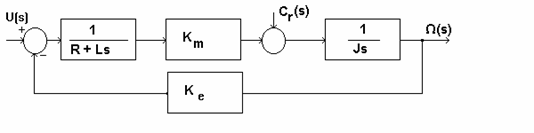
Figura 3.4 - Schema echivalenta a MCC
Iesirea in acest model este turatia. Din punct de vedere al proiectantului pentru alegerea turatiei se utilizeaza doua functii de transfer ca in figura urmatoare:

Figura 3.5
Pentru schemele de mai sus avem urmatoarele functii de transfer:
![]() H(s)=H1(s) · H2(s)
H(s)=H1(s) · H2(s)
![]() si
si ![]()
Sau explicitand relatiile:
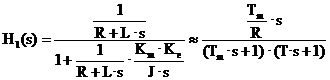
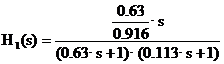
![]()
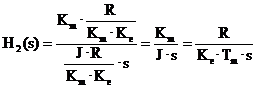
unde ![]()
![]()
![]()
Din punct de vedere practic functia de transfer al motorului s a divizat in doua functii de transfer. Aceasta subdivizare s-a facut pentru introducerea perturbatiei Cr.
La H1(s) iesirea este curentul rotoric Ia si intrarea tensiunea Ua. Se evidentiaza doua constante de timp care se exprima in secunde:
![]() = 0.113 [s
= 0.113 [s
![]() -
-
![]()
Se observa ca Tm >>T astfel H1(s) devine:
![]()
![]()
![]() depinde atat de
parametri electrici Ke, R cat si de parametrii mecanici J, Kmsi
are o valoare mai mare decat T.
depinde atat de
parametri electrici Ke, R cat si de parametrii mecanici J, Kmsi
are o valoare mai mare decat T.
La functia de transfer H2(s) se remarca prezenta unui pol in origine, deci procesul condus, motorul, contine un integrator care imbunatateste precizia sistemului (reduce eroarea stationara). Pe de alta parte intrucat sistemul are si o reactie negativa motorul de curent continuu e un sistem stabil de ordinul doi cu amortizare, care depinde de parametrii motorului.